图形学第一定理：如果看起来结果是对的，那么就是对的
If it looks right, it is right.

#二维笛卡尔坐标系

对于二维坐标而言，无论 X 轴和 Y 轴选取的方向如何，都能通过旋转（包括翻转）将其互相转换。

以 X 轴为第一个轴，它有 4 种选择（上、下、左、右），此时因为 Y 轴必须与 X 轴垂直，因此 Y 轴只有两种可能（正向或反向），因此二维坐标系一共有 8 种可能， 如下图所示：
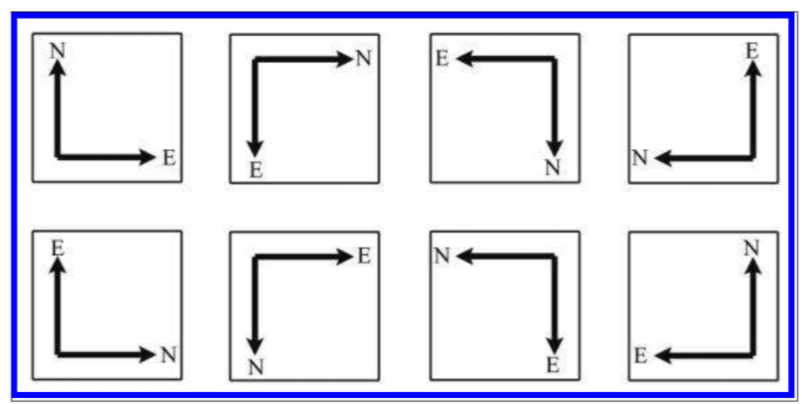
二维坐标系

对上述的 8 个二维坐标系，挑选任意一个，剩下的七个都可以通过旋转或反转或两者的结合，将其转换到挑选的坐标系，也因此从某种角度而言，二维坐标系只有一个。

#三维笛卡尔坐标系

三维坐标一共有 48 种可能 —— Z 轴一共有 6 种可能，X 和 Y 构成二维坐标有 8 种可能，因此一共 有 6∗8=486*8 = 48 种可能。

对于三维坐标而言，可以通过旋转或反转或两者的结合将三维坐标系中的两个坐标轴匹配，但当两个坐标轴匹配后，第三个坐标轴的方向必然是反的。因此所有的三维坐标被分为两组，一组被称为左手坐标系（Left-handed coordinate spaces），另一组被称为右手坐标系（Right-handed coordinate spaces），如下所示：
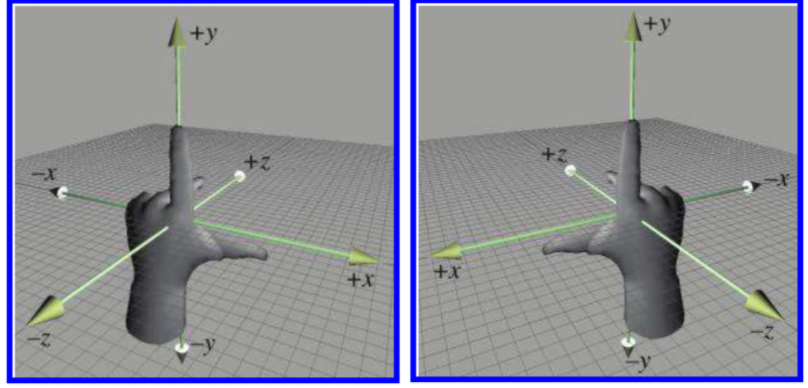
左手、右手坐标系

左右手坐标系只是不同的选择，两者并无其他方面的差异。

之所以用左右手系称呼，是因为可以用手势表示不同的坐标系，如上图所示:食指，中指，大拇指相互垂直，大拇指指向 X 轴正方向，食指指向 Y 轴正方向，中指指向 Z 轴正方向。

  • 左右手坐标系还会影响旋转的正方向:在每个坐标系下，如果要绕着某个轴旋转，用大拇指指向该轴的正方向，四指环绕方向即为旋转的正方向。

本书中使用的坐标系都是左手坐标系

#小零碎数学

#角度，度，弧度

要描述角度（Angles）通常有两种单位，其中度（Degrees）在日常生活中用的比较多，在数学上弧度（Radians）用的更多。

当提及弧度，实际上是计算某角度在半径为 1 的圆上所占的长度。因为半径为 1 的圆周长为 2π2\pi，所以360∘=2π(rad)360^\circ = 2\pi (rad) ，即度与角度的转换关系如下：

1 rad=(180/π)∘≈57.29578∘1∘=(π/180) rad≈0.01745329 rad1\text{ rad} = (180/\pi)^\circ \approx 57.29578^\circ \\\\ 1 ^ \circ = (\pi /180) \text{ rad} \approx 0.01745329 \text{ rad}

#三角函数

对于在半径为 1 的圆上的点 (x,y)(x,y)，θ\theta 为该点与原点形成的向量与 xx 轴正方向的夹角，即：
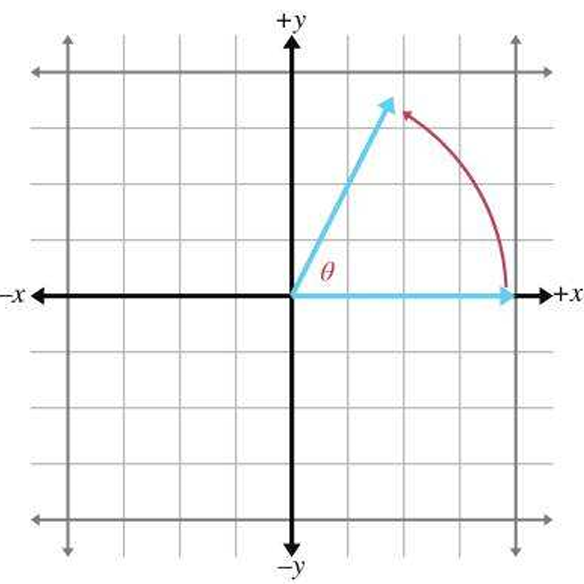
三角函数 | 500

x=cos⁡(θ)y=sin⁡(θ)\begin{aligned} x = \cos(\theta) \\ y = \sin(\theta) \end{aligned}

将 rr 定义为点 (x,y)(x,y) 到原点的距离，则有：
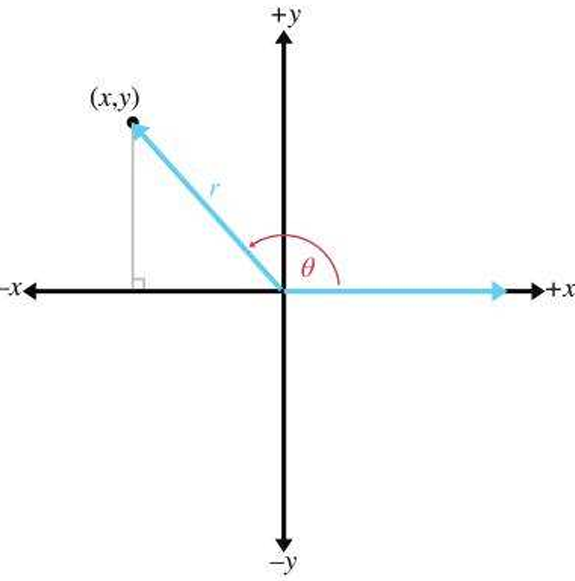
三角函数 | 300

cos⁡θ=x/r,sin⁡θ=y/r,tan⁡θ=y/xsec⁡θ=r/x,csc⁡θ=r/y,cot⁡θ=x/y\begin{array}{lll} \cos \theta=x / r, & \sin \theta=y / r, & \tan \theta=y / x \\ \sec \theta=r / x, & \csc \theta=r / y, & \cot \theta=x / y \end{array}

#三角恒等式

#基本转换

sin⁡(−θ)=−sin⁡θ cos(−θ)=cos⁡θtan⁡(−θ)=−tan⁡θsin⁡(π2−θ)=cos⁡θcos⁡(π2−θ)=sin⁡θtan⁡(π2−θ)=cot⁡θcos⁡θ=−cos⁡(180−θ)sin⁡θ=sin⁡(180−θ)\begin{aligned} \sin(-\theta)=-\sin\theta \\\\\ cos(-\theta)=\cos\theta \\\\ \tan(-\theta)=-\tan\theta \\\\\sin(\frac{\pi}{2}-\theta) = \cos\theta\\\\\cos(\frac{\pi}{2}-\theta) = \sin\theta\\\\\tan(\frac{\pi}{2}-\theta) = \cot\theta\\\\\cos \theta = -\cos(180-\theta)\\\\\sin \theta = \sin (180-\theta) \end{aligned}

#勾股定理

sin⁡2θ+cos2θ=1  1+tan⁡2θ=sec⁡2θ  1+cot⁡2θ=csc2θ\begin{aligned} \sin^2\theta+cos^2\theta=1 \\\\   1 + \tan^2\theta = \sec^2\theta \\\\   1 + \cot^2\theta = csc^2 \theta \end{aligned}

#加减定理

sin⁡(a+b)=sin⁡acos⁡b+cos⁡asin⁡bsin⁡(a−b)=sin⁡acos⁡b− cosasin⁡bcos⁡(a+b)=cos⁡acos⁡b−sin⁡asin⁡bcos⁡(a−b)=cos⁡acos⁡b+sin⁡asin⁡btan⁡(a+b)=tana+tanb1−tan⁡atan⁡btan⁡(a−b)=tana−tanb1+tan⁡atan⁡b\begin{aligned} \sin(a+b) = \sin a \cos b + \cos a\sin b \\\\\sin(a-b) = \sin a \cos b - \ cos a \sin b \\\\\cos(a+b) = \cos a \cos b -\sin a \sin b \\\\\cos(a-b) = \cos a \cos b + \sin a \sin b \\\\\tan(a+b) = \frac{tan a+ tan b}{1- \tan a\tan b } \\\\\tan(a-b) = \frac{tan a - tan b }{1+ \tan a \tan b} \\\\ \end{aligned}

#两倍角定理

sin⁡2θ=2sin⁡θcos⁡θcos⁡2θ=cos⁡2θ−sin⁡2θ=2cos2θ−1=1−2sin2θtan⁡2θ=2tan⁡θ1−tan⁡2θ\begin{aligned} \sin 2\theta = 2\sin \theta \cos \theta \\ \cos 2\theta = \cos ^2 \theta-\sin^2\theta=2cos^2\theta-1=1-2sin^2\theta \\ \tan 2 \theta=\frac{2\tan \theta}{1- \tan^2\theta} \\ \end{aligned}

#正弦定理

对于如下三角形：

正弦定义

有以下关系：

sin⁡Aa=sin⁡Bb=sin⁡Cc\frac{\sin A}{a} = \frac{\sin B}{b}=\frac{\sin C}{c}

#余弦定理

对上示的三角形，有：

a2=b2+c2−2bccos⁡Ab2=a2+c2−2accos⁡Bc2=a2+b2−2abcos⁡C\begin{aligned} a^2=b^2+c^2-2bc\cos A \\\\ b^2 = a^2 +c^2 - 2ac \cos B\\\\ c^2 = a^2 +b^2 -2ab \cos C \\ \end{aligned}