《3D 数学基础》 第二章 向量

#向量的数学定义

从数学角度看

• 向量（Vector）只是一个数字的数组。
• 向量（vector）带有方向， 标量（scalar） 不带有方向。
  • 如速度（有朝着某方向的含义在）是向量，位移是向量，
  • 速率（仅仅是一个数字）是标量，距离是标量。

向量的维度表示一个向量中含有多少个数字。

向量通常通过方括号包裹，如果向量是水平方向的写，称其为行向量，否则为列向量，如：

行向量：

$$[1,2,3]$$

列向量：

$$\left[\begin{array}{l} 1 \\ 2 \\ 3 \end{array}\right]$$

研究向量和矩阵的数学称为 线性代数（linear algebra），在线性代数中，$n$维度的向量和矩阵是用来求解有$n$个未知数的方程的。

但在图形学中，更多关注于向量和矩阵的几何意义。

#向量的几何意义

从几何角度来说，向量是一条既有大小又有方向的线（有向线）。

向量并没有位置信息，大小和方向一致的向量出现在图中的什么位置并没有区别。

#笛卡尔坐标系中的向量

#表示位移的向量

当向量出现在笛卡尔坐标系中，向量中的每个元素表示对应的坐标轴的位移。

• 如 $[2,3]$ 表示沿着 $x$ 轴方向移动了 2，沿着 $y$ 轴方向移动了 3，位移的顺序并没有关系。

#零向量

零向量是唯一一个没有方向的向量，在坐标系中，零向量不是一根线，而是一个点。

零向量是作为 加法单位元（additive identity），即加到别的元素上也不会造成区别的数字。

#向量与点

点（Points）表示位置， 向量（Vectors） 表示位移。

#向量和点的关系

向量 $[x,y]$ 表示从原点到点 $(x,y)$ 的位移。

点是位置，图像上表示为一个点。向量是位移，图像上表示为一个箭头。

#向量求反

#数学定义

向量求反（Vector negating）：对于每个向量，都有一个相同维度的反向量，满足 $v+(-v)=0$ 。

向量取反：

$$-\begin{bmatrix}a\\\\a_2 \\\\\vdots \\\\a_{n-1} \\\\a_n \\\\\end{bmatrix}=\begin{bmatrix}-a_1 \\\\-a_2 \\\\\vdots \\\\-a_{n-1} \\\\-a_n \\\\\end{bmatrix}$$

#几何意义

向量求反几何意义：保持向量的大小，但是方向变反方向

#向量与标量相乘

#数学定义

向量与标量相乘：

$$k\begin{bmatrix}a_1 \\\\a_2 \\\\\vdots \\\\a_{n-1} \\\\a_n \\\\\end{bmatrix}=\begin{bmatrix}a_1 \\\\a_2 \\\\\vdots \\\\a_{n-1} \\\\a_n \\\\\end{bmatrix}k=\begin{bmatrix}ka_1 \\\\ka_2 \\\\\vdots \\\\ka_{n-1} \\\\ka_n \\\\\end{bmatrix}$$

• 向量与标量相乘，标量可以写在向量的左侧也可以写在右侧，但通常而言习惯性写在右侧
• 向量与标量相乘时不需要写乘号
• 标量不能被向量除，向量不能除以另一个向量。

#几何意义

向量与标量相乘几何意义：大小乘以$|k|$，如果$k$是负数，则向量的方向取反，否则不变。

#向量加法和减法

#数学定义

向量相加：

$$\left[\begin{array}{c}a_{1} \\a_{2} \\\vdots \\a_{n-1} \\a_{n}\end{array}\right]+\left[\begin{array}{c}b_{1} \\b_{2} \\\vdots \\b_{n-1} \\b_{n}\end{array}\right]=\left[\begin{array}{c}a_{1}+b_{1} \\a_{2}+b_{2} \\\vdots \\a_{n-1}+b_{n-1} \\a_{n}+b_{n}\end{array}\right]$$

向量相减：

$$\left[\begin{array}{c}a_{1} \\a_{2} \\\vdots \\a_{n-1} \\a_{n}\end{array}\right]-\left[\begin{array}{c}b_{1} \\b_{2} \\\vdots \\b_{n-1} \\b_{n}\end{array}\right]=\left[\begin{array}{c}a_{1} \\a_{2} \\\vdots \\a_{n-1} \\a_{n}\end{array}\right]+\left(-\left[\begin{array}{c}b_{1} \\b_{2} \\\vdots \\b_{n-1} \\b_{n}\end{array}\right]\right)=\left[\begin{array}{c}a_{1}-b_{1} \\a_{2}-b_{2} \\\vdots \\a_{n-1}-b_{n-1} \\a_{n}-b_{n}\end{array}\right]$$

向量不能与标量相加或相减，也不能与维度不同的向量相加或相减

#几何意义

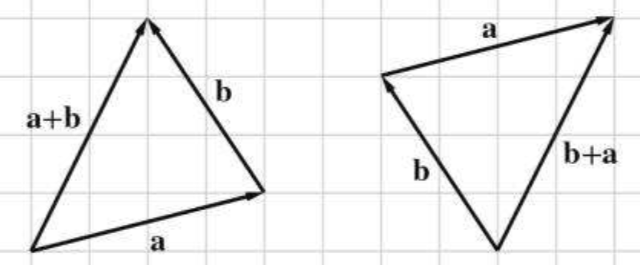
向量相加几何意义：如果是向量 $a+b$，可以将 $a$的头部与$b$的尾部向量，从$a$的尾部指向$b$的头部的向量即为加法结果，如下所示：

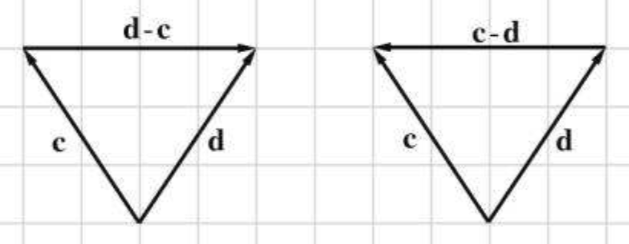
向量相减几何意义：如果向量 $d-c$，则将两个向量的尾部向量，从 $c$ 头部指向 $d$ 头部的向量即为减法结果，如下图所示：

#从一个点移动到另一个点

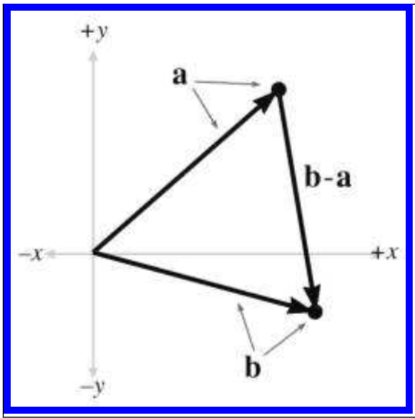
当要计算从点 $a$ 到点 $b$ 的位移向量，可以通过 $b-a$ 获得，如下图所示：

#向量长度

#数学定义

向量的大小也常称为向量的 长度（Length）或向量的 模（Norm）。

求向量的大小：

$$\|\mathbf{v}\|=\sqrt{\sum_{i=1}^{n} v_{i}^{2}}=\sqrt{v_{1}^{2}+v_{2}^{2}+\cdots+v_{n-1}^{2}+v_{n}^{2}}$$

如果有向量 $a$和 $b$，则 $a,b$ 满足：

$$\begin{aligned} \Vert a \Vert^2 + \Vert b \Vert^2 = \Vert a+b \Vert^2 \\ \Vert a \Vert + \Vert b \Vert\geq \Vert a+b \Vert \end{aligned}$$

#几何意义

向量大小几何含义：求向量 $v$ 的大小，等同于求以向量 $v$ 为斜边的直角三角形的斜边长度。

• 假设存在向量 $v=[3,4]$，则 $v$ 的模长为 $\sqrt{3^2+4^2}=\sqrt{9+16}=\sqrt{25}=5$。

#单位向量

#数学定义

单位向量（Unit vector）是长度为 1 的向量（并没有限定方向），单位向量也被称为 归一化向量（normalized vectors）。

normalized vector 表示是归一化向量即单位向量，即长度为 1 的向量。normal vector 表示法向量，是垂直于某个面的向量。

某个方向上的单位向量可以通过这个方向上的某向量除以它的大小得到，即：

$$\hat = \frac{v}{\Vert v \Vert}$$

零向量不能被归一化

#几何意义

单位向量几何意义：

• 在二维坐标系中，如果将无数的单位向量的尾部放在原点，则其顶点可以构成半径为 1 的圆。
• 在三维坐标系中，如果将无数的单位向量的尾部放在原点，则其顶点可以构成半径为 1 的球。

#距离公式

求两向量的距离：

$$\operatorname{distance}(\mathbf{a}, \mathbf{b})=\|\mathbf{b}-\mathbf{a}\|=\sqrt{\left(b_{x}-a_{x}\right)^{2}+\left(b_{y}-a_{y}\right)^{2}+\left(b_{z}-a_{z}\right)^{2}}$$

#向量点乘

#数学定义

向量点乘（dot product）又称为 向量内积（inner product）

向量点乘时必须用一个使用点符号，如 $a \cdot b$，计算如下：

$$\left[\begin{array}{c}a_{1} \\a_{2} \\\vdots \\a_{n-1} \\a_{n}\end{array}\right] \cdot\left[\begin{array}{c}b_{1} \\b_{2} \\\vdots \\b_{n-1} \\b_{n}\end{array}\right]=a_{1} b_{1}+a_{2} b_{2}+\cdots+a_{n-1} b_{n-1}+a_{n} b_{n}$$

如果两个向量之间没有点符号，则会认为这两个向量要进行矩阵的乘法

• 向量的点乘是相互的，即：

$$a\cdot b=b \cdot a$$

• 向量的点乘可以与标量的乘法相结合，即：

$$(ka)\cdot b =k(a\cdot b)=a\cdot(kb)$$

• 向量的点乘满足加法与减法的分配律，即：

$$a\cdot(b+c)=a\cdot b+a\cdot c$$

#几何意义

#投影

• 点乘的第一个几何意义—— 投影：

假设 $a$ 是单位向量，则 $a$ 与 $b$ 的点乘， $\hat{a}\cdot b$表示为$b$在$a$上的投影的有向长度

• 因为点乘的结果是标量，所以这里的有向指的是正负，而不是方向
• 当为负数时，表示的是 $b$ 在 $\hat{a}$ 上的投影点，是在 $\hat{a}$ 的反方向上

向量 $a$ 与向量 $b$ 的点乘，结果为向量 $b$ 在向量 $a$ 上的有向投影长度（ $b$ 的长度会影响该投影长度）乘以向量 $a$ 的长度。

#计算分量

• 点乘的第二个几何意义——计算分量：

$b$ 在 $a$ 上的投影可以看作是 $b$ 在 $a$ 方向上的分量。因此还可以通过投影来将 $b$ 拆分为两部分，平行于 $a$ 的分量和垂直与 $a$ 的分量，即：

$$\begin{array}{c}b_{\|}=(\hat{a} \cdot b) \hat{a} \\ b_{\perp}=b-(\hat{a} \cdot b) \hat{a}\end{array}$$

#计算角度

• 点乘的第三个几何意义——计算角度

  两个向量的点积等于这两个向量之间夹角的$cos$乘上两个向量的大小，即：

  $$\begin{array}{r}a \cdot b=\|a\|\|b\| \cos \theta \\\theta=\arccos \left(\frac{a \cdot b}{\|a\|\|b\|}\right)\end{array}$$

如果点乘的两个向量夹角范围在 $-90^\circ \sim 90^\circ$ ，结果为正数。 如果夹角为 90°，结果为 0。 如果范围在 $90^\circ \sim 270^\circ$，结果为负数。
结果是正数，意味着两向量指向同一个方向（比如都往前），结果是负数则表示指向不同方向（一个向前，一个向后）。

#向量叉乘

向量与向量还有个计算称为 叉乘（Cross product）。

#Official Linear Algebra Rules

以三维向量的叉乘为例，表达式及计算如下：

$$\left[\begin{array}{l}x_{1} \\y_{1} \\z_{1}\end{array}\right] \times\left[\begin{array}{l}x_{2} \\y_{2} \\z_{2}\end{array}\right]=\left[\begin{array}{l}y_{1} z_{2}-z_{1} y_{2} \\z_{1} x_{2}-x_{1} z_{2} \\x_{1} y_{2}-y_{1} x_{2}\end{array}\right]$$

• 当向量和点乘一起发生时，先计算叉乘，再计算点乘，即：

  $$a \cdot b \times c=a \cdot(b \times c)$$

  • 形如$a\cdot (b\times c)$的表达式称为三重积。

• 叉乘是反交换的，即：

  $$a\times b = -(b\times a)$$

• 叉乘满足分配律，即：

  $$a\times(b+c)=a\times b + a\times c$$

• 叉乘没有结合律，即：

  $$(a \times b)\times c \neq a\times(b\times c)$$

• 标量可以与叉乘相结合，即：

  $$k(a\times b)=(ka)\times b = a\times(kb)$$

#几何意义

叉乘返回的结果是垂直于两个叉乘向量的另一个向量，如下图所示：

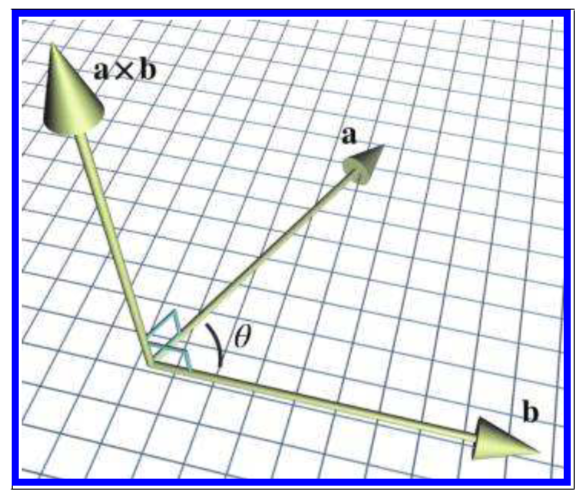
结果的大小等于两个向量的大小乘上两个向量之间夹角的 $sin$ ：

$$\Vert a\times b \Vert = \Vert a\Vert \Vert b\Vert \sin \theta$$

该大小也等于由两个向量构成的平行四边形的面积。

结果的方向与左右手坐标系相关，如果表达式为 $a \times b$ ，将 $b$ 的尾部与 $a$ 的头部相连。 在左手坐标系下，如果在形成的方向是顺时针的，则结果方向指向外侧，如果是逆时针，则指向内侧。 在右手坐标系下，结果相反。如下图所示：

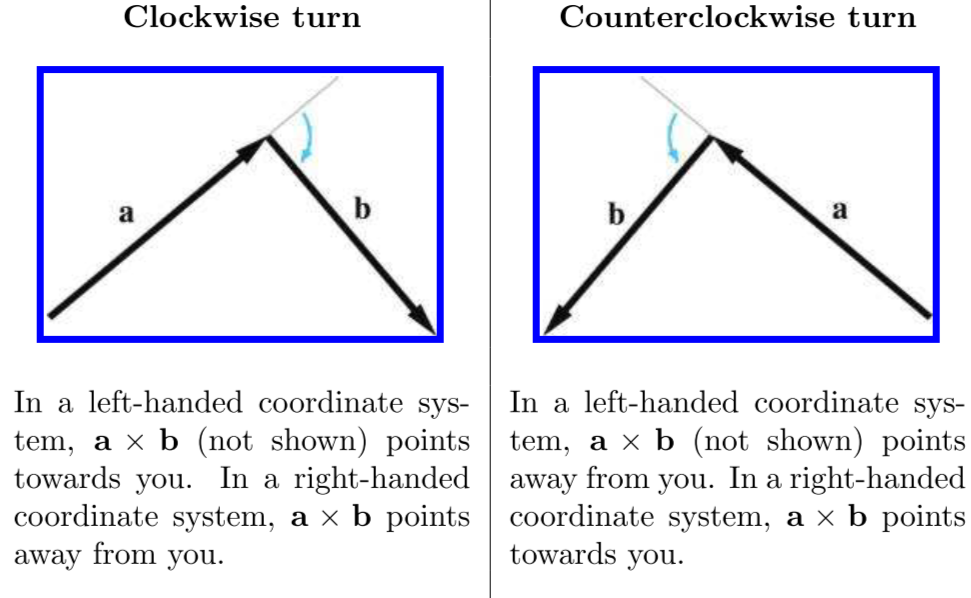
也可以用手指来求叉乘结果方向，如果表达式为$a \times b$，将大拇指指向 $a$ 的方向，将食指指向 $b$ 的方向，让中指与食指和大拇指垂直（像展示左右手坐标系那样），中指的方向即为叉乘结果方向。