《3D 数学基础》 第三章 坐标系
#一些有用的坐标系
之所以需要不同的坐标系,是因为一些信息仅在某些坐标系下是有意义的,或者只能在某坐标系下获得,或更容易得到。
#世界坐标系
世界坐标系(World Spaces)是作为一个全局的存在,所有的其他坐标系都属于这个坐标系下。世界坐标系是需要关心的最大坐标系(类似于全集的概念)。
世界坐标系也被称为 全局坐标系(Global coordinate space)或者 统一坐标系(Universal coordinate space)。
#物体坐标系
物体坐标系(Object Space)是属于每一个物体的,即每个物体都有自己的物体坐标系,当这个物体移动时,物体坐标系也相应移动。
“向右转”就是物体坐标系的概念,而“向东走”就是全局坐标系的概念。
在图形学中,物体坐标系也被称为 模型坐标系(Model Space),或本地坐标系(Local Space)模型的顶点信息就描述在该物体的模型坐标系下。
#摄像机坐标系
物体坐标系的一个重要特例就是 摄像机坐标系(Camera Space),摄像机坐标系是关于用于渲染的视角的坐标系。
针对 Camera 这一游戏物体的物体坐标系,我们称之为摄像机坐标系。
在摄像机坐标系下, 轴指向右侧, 轴指向前方,指向上方
摄像机坐标系如下图所示: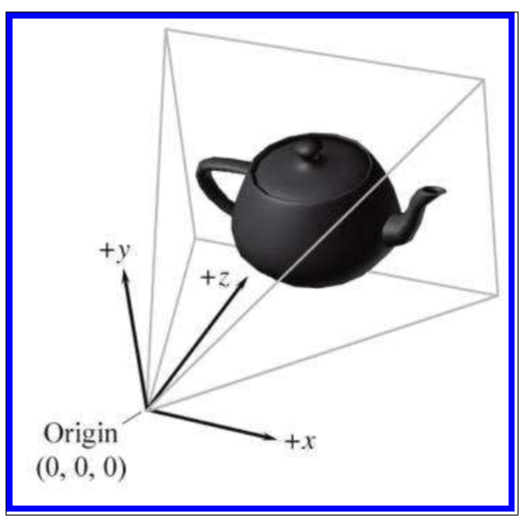
#直立坐标系
直立坐标系(Upright space)是这本书中提出的概念(在其他的教程或书籍中看不到这个概念),是作为世界坐标和物体坐标转化过程中的中间变量存在,如下图所示: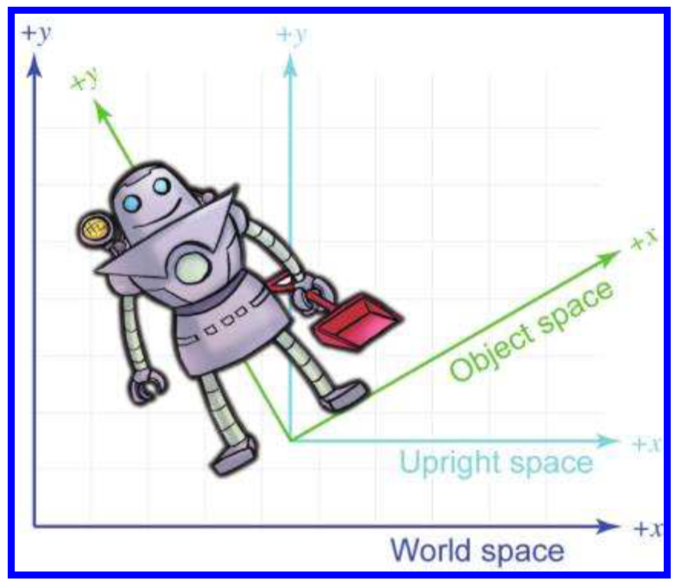
直立坐标系的原点与物体坐标系相同,直立坐标系的方向与世界坐标系相同。
下图为物体坐标系与世界坐标系经过直立坐标系转换的步骤: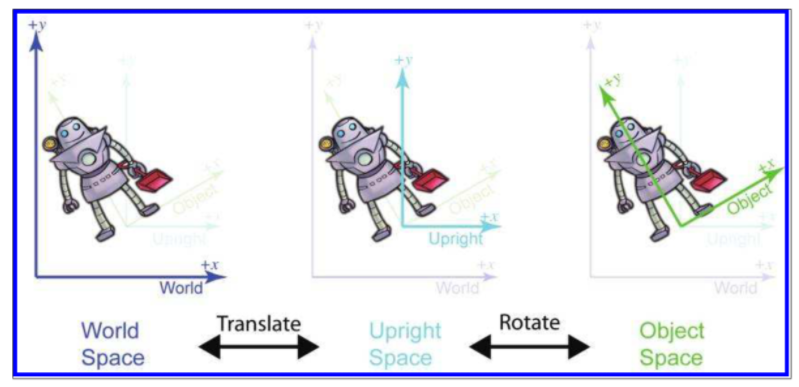
#基本向量和坐标系转换
将一个坐标系下的坐标转换为另一个坐标系下的坐标称为 坐标系转换(coordinate space transformation)。
#坐标系转换的两种角度
坐标系转换可以从两个角度来考虑:
- 主动转换(Active Transformation):两个坐标系保持不动,物体的坐标进行转换
- 被动转换(Passive Transformation):物体保持不动,坐标系进行转换
只需要注意的是,在从两个角度思考时,位移的方向是不同的。如上图从世界坐标转换到直立坐标系的过程:
- 如果思考角度是移动物体,那么物体是向左下移动,到了原点;
- 如果是从移动坐标系角度考虑,坐标系是向右上移动,到了原点。
另一点是,在进行旋转操作时,要保证物体处于当前坐标系的原点,因为一个坐标系下的旋转操作都是基于该坐标系的原点的。
所以在上图中,当从世界坐标系转换到本地坐标系时,会先移动转换到直立坐标系,因为前者坐标系物体不在原点,而后者在。同理在从本地坐标系转换到世界坐标系时,会先进行旋转,因为此时物体已经在原点了。
直立坐标系的引入,是为了引入一个中间坐标系以保证“进行旋转时,物体在当前坐标系的原点”。
#定义一个坐标系
坐标系是由原点和坐标轴两部分决定的,而一个坐标系的 原点和 坐标轴又是相对于另一个坐标系的。
如在展示三个坐标系的上图中:如果说机器人的高度是。那么
直立坐标系的原点在世界坐标系中的位置大约在 。
物体坐标系中的点,在直立坐标系下大约是。
物体坐标系中的点,在直立坐标系下大约是。
在直立坐标系中,向量的角度大约是 。
因此两个坐标系的原点位差距为,角度差距在 。
#向量转换公式
如果想要将一个坐标系下的点转换到另一个坐标系下,可以按以下公式进行计算:
其中:
表示原坐标系下点的位置
表示该点在转换后的坐标系下的位置
为原坐标系的原点在新坐标系中的位置
为原坐标系下的 轴在新坐标系下的表示, 为原坐标系下的 轴在新坐标系下的表示, 为原坐标系下的 轴在新坐标系下的表示。
如果求的是一个坐标系下的向量转换到另一个坐标系下,则可以无视掉
#嵌套坐标系
因为通常而言,物体坐标系最后都要基于世界坐标系进行计算,如把不同的物体放在世界中的过程。
因此可以称世界坐标系是父空间,物体坐标系是子空间。
而物体坐标系可以进一步划分,如将一只羊作为物体坐标系,可以再进一步将其头作为物体坐标系的子坐标系,称为头坐标系。同理头坐标系下还可以耳朵坐标系等。
这种将不同部分层层划分的模型称为 关节模型(articulated model)。
一些运动在各自的坐标系下计算是很简单的,但是放在世界坐标系下将会很复杂。如羊一边走,一边摇头,一边上下翻动耳朵。对于耳朵坐标系而言,这只是 Y 轴的变化,但是对于世界坐标系而言,就是耳朵的运动轨迹就非常复杂了。

