#矩阵的数学定义

在线性代数中，矩阵是由一系列数字按行和列排布组成。

可以将向量看作是标量的集合，把矩阵看作是向量的集合。

#矩阵的维度和表示方法

将一个有 rr 行，cc列的矩阵称为是 r×cr\times c 矩阵，矩阵中的数字由方括号包围，如下为一个 3×33 \times 3 的矩阵：

M=[m11m12m13m21m22m23m31m32m33]M=\begin{bmatrix}m_{11}&m_{12}&m_{13}\\\\m_{21}&m_{22}&m_{23}\\\\m_{31}&m_{32}&m_{33}\\\\\end{bmatrix}

#方阵

将行数和列数相同的矩阵，称为方阵（Square Matrices）。

将下标的行数和列数相同的元素，称为对角元素（Diagonal elements），如上矩阵中的m11m_{11}，m22m_{22}，m33m_{33}为对角元素。

如果一个矩阵（并不一定是方阵）中，所有的非对角元素都是 0，那么整个矩阵称为 对角矩阵（diagonal matrix） ，如下所示：

M=[m11000m22000m33]M=\begin{bmatrix}m_{11}& 0 & 0\\\\0 &m_{22}& 0\\\\0 &0 & m_{33}\\\\\end{bmatrix}

在对角矩阵中，如果所有的元素都为 1，那么就变成了单位矩阵（Identity Matrix），单位矩阵通常用 I\mathbf{I} 表示，如下所示：

I3=[100010001]\mathbf{I}_{3}=\left[\begin{array}{lll} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right]

如果一个矩阵与单位矩阵相乘，那么得到的还是该矩阵本身。

#向量视作矩阵

向量可以看作是一个 1×n1\times n 或者 n×1n \times 1 的矩阵，即 1×n1\times n 的矩阵可以称为行向量，n×1n\times 1 可以称为列向量。

#向量转置

给定一个 r×cr\times c 矩阵 M\mathbf{M}，其转置写为 MT\mathbf{M^T}，转置矩阵是一个 c×rc\times r 的矩阵。其中 M\mathbf{M} 中的 行 变为 MT\mathbf{M^T} 中的 列 ，即MijT=Mji\mathbf{M^T_{ij}}=\mathbf{M_{ji}}，如下：

[abcdefghi]T=[adgbehcfi]{\begin{bmatrix}a&b&c\\\\d&e&f\\\\g&h&i\\\\\end{bmatrix}}^T=\begin{bmatrix}a&d&g\\\\b&e&h\\\\c&f&i\\\\\end{bmatrix}

[xyz]T=[xyz]{\begin{bmatrix}x & y &z\end{bmatrix}}^T=\begin{bmatrix}x\\\\y\\\\z\\\\\end{bmatrix}

转置矩阵有如下性质：

  1. 矩阵转置的转置等于本身，(MT)T=M(\mathbf{M^T})^T=\mathbf{M}
  2. 如果一个矩阵的转置等于矩阵本身，那么 DT=D\mathbf{D^T}=\mathbf{D}，那么这个矩阵就是是单位矩阵。

#矩阵与标量相乘

矩阵与标量的相乘如下表示：

kM=k[m11m12m13m21m22m23m31m32m33]=[km11km12km13km21km22km23km31km32km33]kM=k\begin{bmatrix}m_{11}&m_{12}&m_{13}\\\\m_{21}&m_{22}&m_{23}\\\\m_{31}&m_{32}&m_{33}\\\\\end{bmatrix}=\begin{bmatrix}km_{11}&km_{12}&km_{13}\\\\km_{21}&km_{22}&km_{23}\\\\km_{31}&km_{32}&km_{33}\\\\\end{bmatrix}

#两个矩阵相乘

对于 r×nr\times n 的矩阵 A\mathbf{A}，如果与 n×cn\times c 的矩阵 B\mathbf{B} 相乘，结果为 r×cr\times c 的矩阵 AB\mathbf{AB}

对于两个矩阵相乘，前者的列数必须与后者的行数匹配

假设将两个矩阵的相乘结果中的每个元素称为 cijc_{ij}，其值为第一个矩阵的的第ii行中所有元素与第二个矩阵的第jj列中的元素一一相乘并累加，即：
矩阵相乘图解

矩阵相乘有如下性质：

  1. MI=IM=M\mathbf{MI=IM=M}
  2. 矩阵的相乘不是可交换的，AB≠BA\mathbf{AB\neq BA}
  3. 矩阵的相乘满足结合律，(AB)C=A(BC)\mathbf{(AB)C=A(BC)}。
    矩阵与标量或向量的乘法同样满足结合律，即：

    (kA)B=k(AB)=A(kB)(vA)B=v(AB)\begin{aligned} \mathbf{(kA)B=k(AB)=A(kB)} \\ \mathbf{(vA)B=v(AB)} \end{aligned}

  4. 乘积的转置，等于乘数与被乘数的转置以相反的顺序相乘，(AB)T=BTAT\mathbf{(AB)^T={B^T}{A^T}}

#矩阵与向量相乘

向量与矩阵的乘法如下，行向量与矩阵的相乘：

[xyz][ m11m12m13m21m22m23m31m32m33]=[xm11+ym21+zm31xm12+ym22+zm32xm13+ym23+zm33]\begin{bmatrix}x & y &z\end{bmatrix}\begin{bmatrix}  m_{11}&m_{12}&m_{13}\\\\m_{21}&m_{22}&m_{23}\\\\m_{31}&m_{32}&m_{33}\\\\\end{bmatrix}= \\\\\begin{bmatrix}xm_{11}+ym_{21}+zm_{31} & xm_{12}+ym_{22}+zm_{32} &xm_{13}+ym_{23}+zm_{33}\end{bmatrix}

矩阵与列向量的相乘：

[ m11m12m13m21m22m23m31m32m33][xyz]=[ xm11+ym12+zm13 xm21+ym22+zm23 xm31+ym22+zm33]\begin{bmatrix}  m_{11}&m_{12}&m_{13}\\\\m_{21}&m_{22}&m_{23}\\\\m_{31}&m_{32}&m_{33}\\\\\end{bmatrix}\begin{bmatrix}x\\\\y\\\\z\\\\\end{bmatrix}=\begin{bmatrix}  xm_{11}+ym_{12}+zm_{13}\\\\  xm_{21}+ym_{22}+zm_{23}\\\\  xm_{31}+ym_{22}+zm_{33}\\\\\end{bmatrix}

矩阵和向量的乘法满足分配律， (v+w)M=vM+wM\mathbf{(v+w)M=vM+wM}

#行向量与列向量

行向量与列向量本质上并没有区别，但需要注意使用行列向量与矩阵相乘时的顺序是不同的。

假设向量 v\mathbf{v} 需要与矩阵 A,B,C\mathbf{A,B,C} 依次相乘。如果 v\mathbf{v} 是列向量，那么向量应该出现在右侧，即写为CBAv\mathbf{CBAv}。如果 v\mathbf{v} 是行向量，那么向量应该出现在左侧，即写为vABC\mathbf{vABC}。

行向量与列向量与同一个矩阵相乘后，结果对应的元素是不同的（如行向量计算结果的第一个元素与列向量计算结果的第一个元素不同）。

  • 因此如果想要使用行向量进行计算和使用列向量进行计算的结果向量元素一一对应相等的话，则它们各自使用的矩阵必须是不同的，且为转置关系。

行向量的优点在于，阅读的顺序和相乘的顺序是一致的，即从左到右，而列向量乘积的相乘顺序则是从右到左。

行向量的主要缺点在于，当向量的维度增加时，会让表达式变得非常的长，造成书写的不便，而使用列向量就不会有这个问题。

DirectX使用行向量，OpenGL 和 Unity 使用列向量。 当使用别人的表达式或者代码时，需要特别注意它使用的是行向量还是列向量。

#矩阵的几何意义

从几何意义角度来说，方阵可以描述任何的线性变化（Linear transformation）。

线性变化保证了图形中的线条不会被弯曲，且线条们的平行性质不会给改变，但其他的几何性质，如角度，面积，体积，长度都可能发现变化。线性变化包括：

  1. 旋转(Rotation)
  2. 缩放(Scale)
  3. 正交投影(Orthographic projection)
  4. 反射(Reflection)
  5. 切边（shearing）

#向量和矩阵相乘的几何意义

向量与矩阵相乘后，向量从一个坐标系转换到另一个坐标系：

  • 矩阵可以看作是一个坐标系转换的矩阵
  • 矩阵的每一行可以看作是新坐标系的基本向量

假设 i=[1,0,0],j=[0,1,0],k=[0,0,1]\mathbf{i}=[1,0,0],\mathbf{j}=[0,1,0],\mathbf{k}=[0,0,1]，且矩阵 M\mathbf{M} 为：

[m11m12m13m21m22m23m31m32m33]\left[\begin{array}{lll}m_{11} & m_{12} & m_{13} \\m_{21} & m_{22} & m_{23} \\m_{31} & m_{32} & m_{33}\end{array}\right]

则向量 v\mathbf{v} 可写作 v=vxi+vyj+vzk\mathbf{v}=v_x\mathbf{i}+v_y\mathbf{j}+v_z\mathbf{k} ，且矩阵与向量的乘法可以看作为：

vM=(vxi+vyj+vzk)M=(vxi)M+(vyj)M+(vzk)M=vx(iM)+vy(jM)+vz(kM)=vx[m11m12m13]+vy[m21m22m23]+vz[m31m32m33]\begin{aligned}\mathbf{v} \mathbf{M} &=\left(v_{x} \mathbf{i}+v_{y} \mathbf{j}+v_{z} \mathbf{k}\right) \mathbf{M} \\&=\left(v_{x} \mathbf{i}\right) \mathbf{M}+\left(v_{y} \mathbf{j}\right) \mathbf{M}+\left(v_{z} \mathbf{k}\right) \mathbf{M} \\&=v_{x}(\mathbf{i} \mathbf{M})+v_{y}(\mathbf{j} \mathbf{M})+v_{z}(\mathbf{k M}) \\&=v_{x}\left[\begin{array}{llll}m_{11} & m_{12} & m_{13}\end{array}\right]+v_{y}\left[\begin{array}{lll}m_{21} & m_{22} & m_{23}\end{array}\right]+v_{z}\left[\begin{array}{lll}m_{31} & m_{32} & m_{33}\end{array}\right]\end{aligned}

将上述结果的每一行都看作是一个基本向量，即 [m11m12m13]\begin{bmatrix}m_{11} & m_{12} &m_{13} \end{bmatrix}，[m21m22m23]\begin{bmatrix}m_{21} & m_{22} &m_{23} \end{bmatrix}和[m31m32m33]\begin{bmatrix}m_{31} & m_{32} &m_{33} \end{bmatrix}都作为基本向量，并将他们分别命名为 p,q,r\mathbf{p,q,r}，则上式结果可以改写为：

vM=vxp+vyq+vzr\mathbf{vM}=v_x\mathbf{p}+v_y\mathbf{q}+v_z\mathbf{r}

与原式 v=vxi+vyj+vzk\mathbf{v}=v_x\mathbf{i}+v_y\mathbf{j}+v_z\mathbf{k} 比较，可以得出，原来的基本向量 i,j,k\mathbf{i,j,k} 经过了线性变化，变成了新的基本向量 p,q,r\mathbf{p,q,r}。

不同的的基本向量就构成了不同的坐标系。因此可以将矩阵 M\mathbf{M} 看作是一个坐标系转换的矩阵，它让向量（或点）从由 i,j,k\mathbf{i,j,k} 构成的坐标系转换到由 p,q,r\mathbf{p,q,r} 构成的坐标系。

可以通过上述的方法来直接判断一个矩阵所代表的线性变化，方阵的每一行都是变换后的基本向量，如有方阵：

M=[21−12]\mathbf{M}=\left[\begin{array}{cc}2 & 1 \\-1 & 2\end{array}\right]

其中，p=[21],q=[−12]\mathbf{p}=\begin{bmatrix}2 &1 \end{bmatrix},\mathbf{q}=\begin{bmatrix}-1 &2 \end{bmatrix}。即原坐标(0,1)(0,1)变成了(2,1)(2,1)，原坐标(1,0)(1,0)变成了坐标(−1,2)(-1,2)，如下图所示：
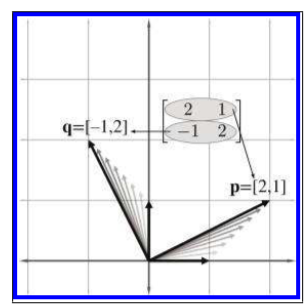
矩阵的每一行都是新坐标系的基本向量

此书中，默认计算的向量都是行向量。如果是计算的向量是列向量，则结论是： 方阵的每一列都是变换后的基本向量

如果对一个二维图片使用该矩阵进行变化，则如下图所示：
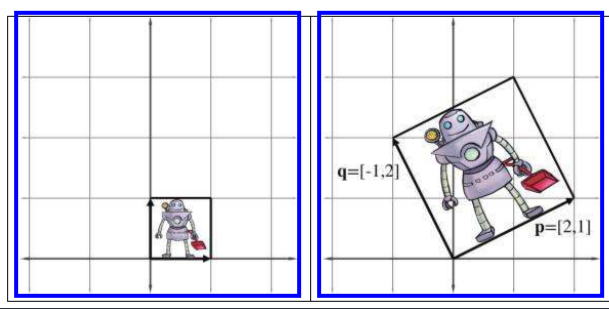
二维矩阵变化

对于三维空间可以同样的方式判断矩阵所表示的线性变化