《Learn OpenGL》 Ch 06 Coordinate System
本部分的实现代码,见 06_CoordinateSystem
#坐标系统
一个物体的顶点数据在最终转换到屏幕坐标系之前要经历多个流程:局部坐标(本地坐标),世界坐标,观察坐标,裁剪坐标,屏幕坐标。
将物体的坐标变换拆成几个过渡坐标系的好处在于,在某些特定的坐标系统中,某些运算将更加方便。
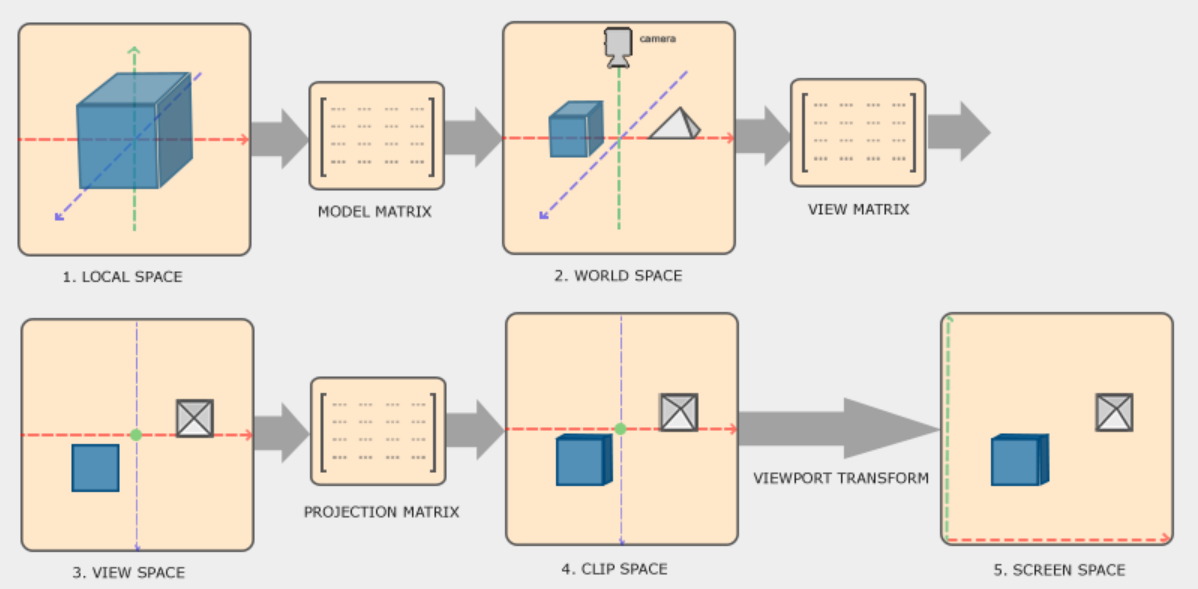
#本地坐标系
本地坐标系是指物体本身的坐标空间,即物体最开始所在的地方。
比如存在一个坐标系,坐标系的 是人的双脚所站的地点,那么他的头的位置可能就是。
#世界坐标系
世界坐标系构建物体在一个世界内的坐标。比如本地坐标中人的头的位置是,那么在一个以房间为世界的坐标中,他双脚的位置可能是,那么头位置就是。
#观察者坐标系
观察坐标是指从观察者角度看到的坐标,观察者以自身作为(0,0,0)点,其他物体相对于这个点的坐标(需要考虑角度,位置,方向)
#裁剪坐标系
裁剪坐标是将能看到的内容映射到 范围后的坐标。映射的过程一般有两种方法: 正射投影(Orthographic)和 透视投影(Perspective)。
只有在透视投影下,才会有近大远小的效果,所以一般来说使用的都是透视投影。
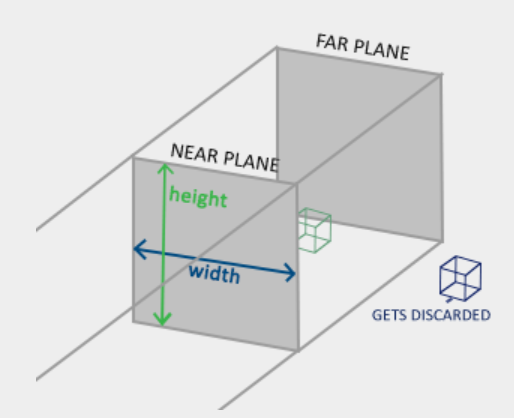
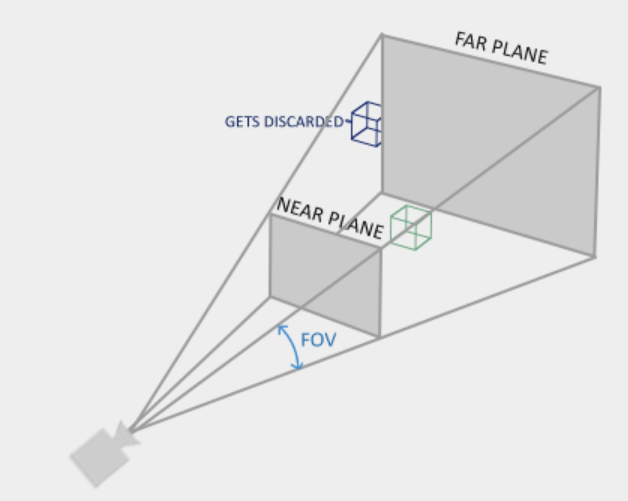
#屏幕坐标
屏幕坐标是以屏幕像素作为基准的坐标系,如果屏幕的分辨率是,且在裁剪坐标系下坐标为 ,则屏幕坐标系下的值为
#变换矩阵
从本地坐标系转换到世界坐标系,需要用到模型矩阵。
从世界坐标系转换到观察者坐标系,需要用到观察矩阵。
从观察者坐标系转换到裁剪坐标系,需要用到投影矩阵。
从裁剪坐标转换到屏幕坐标,通过 OpenGL 的 glViewport 函数完成,并不需要使用矩阵。
#模型矩阵
模型矩阵可通过平移,旋转,缩放等一系列操作完成。如一个物体,在本地坐标系下的位置是 ,在世界坐标系下的位置为。从本地坐标系转换到世界坐标系的过程,实际上就是平移 的操作。
1 | glm::mat4 model; |
位移,旋转,缩放分别通过 translate,rotate 和 scale 进行,如下所示:
1 | glm::mat4 model(1.0f); |
#观察矩阵
观察矩阵在摄像机课程中会详细介绍,这里仅仅做一个摄像机后退的效果。
因为为 OpenGL 是右手坐标系,所以 是朝向前方的。如果要做摄像机后退的效果,实际上等同于场景前移。
1 | glm::mat4 view(1.0f); |
#投影矩阵
glm 中封装了正射投影和透视投影需要的矩阵:平头矩阵和透视投影,两者的使用如下:
1 |
|
投影矩阵的推导可见:Projection Matrix
#矩阵使用
每一个矩阵都应该在顶点着色器中与位置向量相乘,又因为 OpenGL 中矩阵是列向量,所以矩阵是通过左乘连接的。顶点着色器实例代码为:
1 | ... |
CPP 段正常的使用 glUniformMatrix4fv 传递变量即可。
1 |
|
#Cube
之前的课程中,绘制的都是四边形,这里为了更好的体现透视效果,需要绘制一个立方体。
立方体的顶点与索引值定义如下:
1 |
|
这里定义了24个顶点,即每个面使用了4个顶点。理论上,一个立方体只需要定义8个顶点即可画出,因为对于每一个顶点而言,如果只考虑位置,那么它是由三个面共同拥有的。但是这三个面对于这个顶点要求的Texcoord却是不一样的,因此在定义顶点时,需要针对三个面分别定义三个位置相同,但Texcoord不一样的点。因此,一共需要24个顶点才能满足立方体的绘制。
#Z-Buffer
当绘制立方体时,立方体的顶点有着不同的 Z 坐标,即距离摄像机的远近不同。在真实世界中,靠的近的不透明物体会遮挡远的不透明物体。在 OpenGL 中,相同的效果通过 Z-Buffer 实现。
开启 Z-Buffer 的代码如下:
1 | glEnable(GL_DEPTH_TEST); |
在使用了 Z-Buffer 后,每次绘制时就不仅仅需要清理颜色缓存,还需要清理深度缓存:
1 | glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT); |
#结果与源码