#Introduction

这一章讲解释信源（Information Sources）和携带信息的信号的特征。

#Information Sources

数据通信理论更关注于较低层次的通信系统，因此信源可以是任意来源，不仅仅是包括计算机上层的键盘，鼠标，摄像机，传感器等等也是信源。

#Analog And Digital Signals

数据通信由两种信息组成，模拟信息或数字信息。模拟信号是由一个连续变化的函数构成，而数字信号则是跳跃变换的，在某个时间点会从一个强度突然跳跃至另一个强度。下图为模拟信号和数字信号的图解，左为模拟信号，右为数字信号：

模拟信号与数字信号

#Periodic And Aperiodic Signals

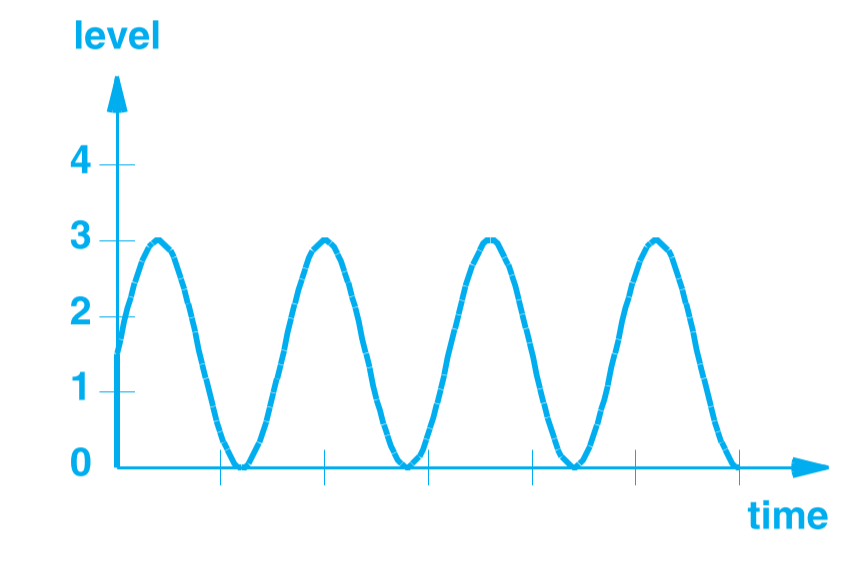
信号也可分类为周期信号与非周期信号。周期信号顾名思义表示信号会重复出现，反之为非周期信号。下图为周期信号：

周期信号

#Sine Waves And Signal Characteristics

数据通信通常使用 Sin函数 来表示信号。之所以选择 Sin 函数，是因为许多自然界产生的信号强度与时间的函数都是 Sin，如麦克风获取声音后的输出信号，电磁波的信号等。

Sin 函数波的信号特性由四个部分组成：

频率（Frequency）：单位时间（通常是秒）内震动出现的个数。单位为赫兹（Hertz,Hz）
波幅（Amplitude）：信号最强和最弱两处的差
相位（Phase）：Sin 拨开始的地方与参考时间（一般是时间 0）的偏移
波长（Wavelength）：一个周期的波在传播媒介中要传播的距离。

其中波长是一个媒介相关的特性，与波在媒介中传播的速度相关。剩下的三个特性都可以用数学公式表示，如波 $A\sin (\omega t+\phi)$ ，其中 $A$ 表示波幅， $\phi$ 表示相位， $\omega$ 表示频率，当 $\omega=2\pi$ 时表示频率为 1。

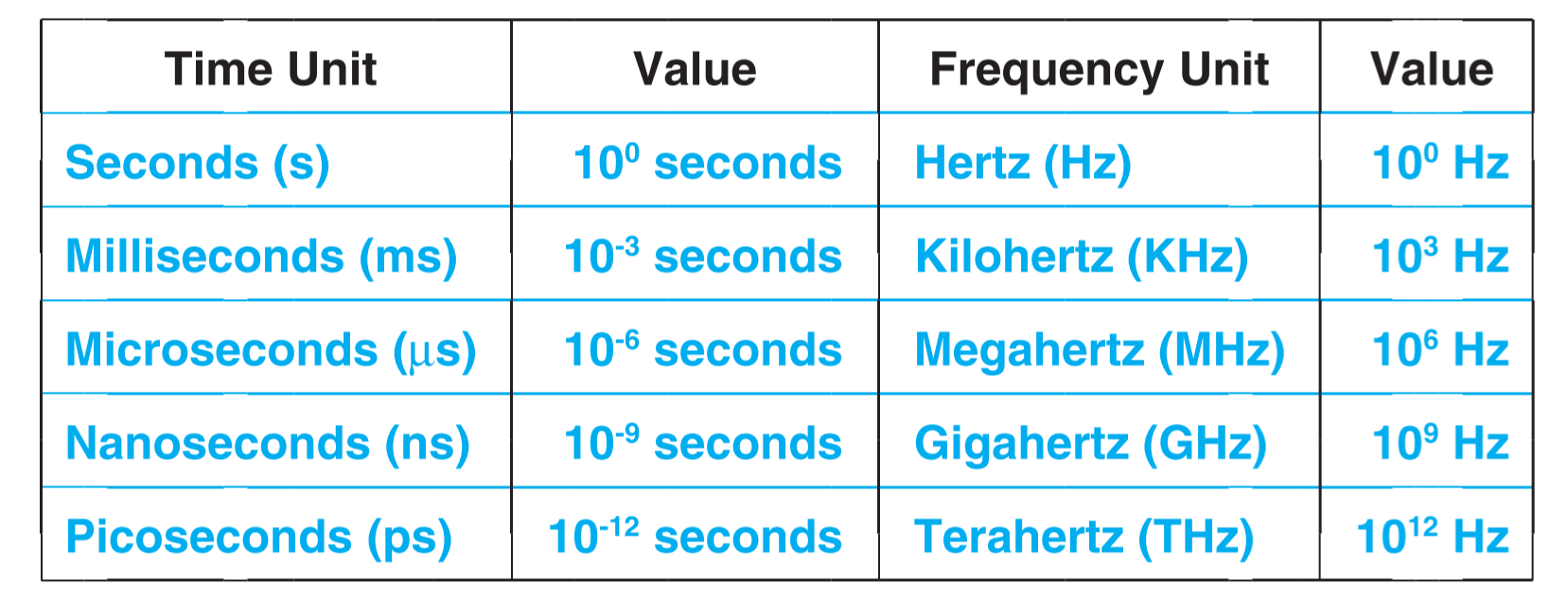
数据通信用的波一般都是高频的，一秒内出现百万个循环，对于这种频率的波，通常用兆赫兹（Megahertz,MHz）来表示。高频率波的单位如下表显示：

频率单位

#Composite Signals

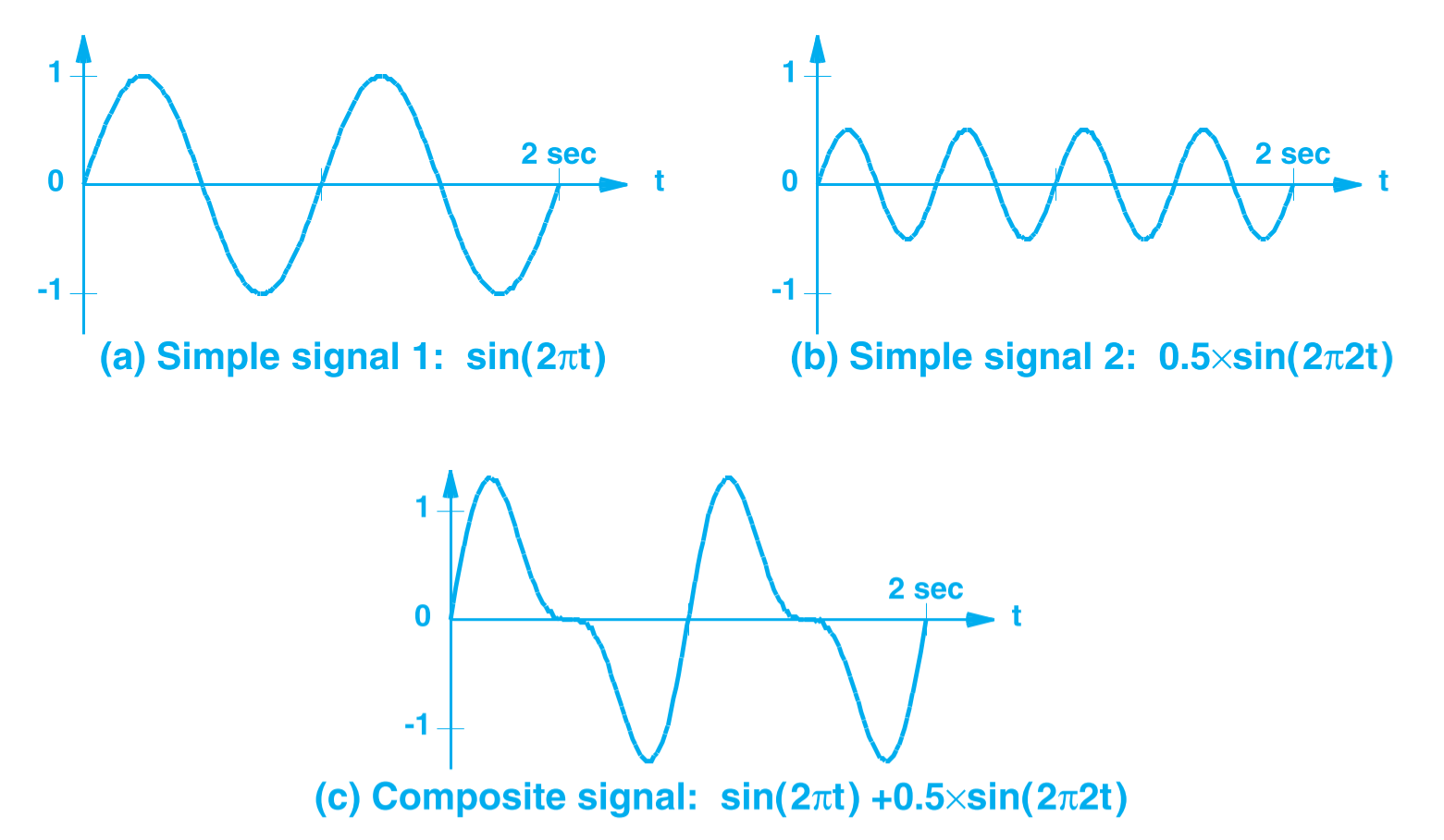
之前图中的波称为简单信号(Simple Signal)，因为只是以单一的 Sin 波组成。但在实际中，多数信号都是以组合信号（Composite Signal）的形式出现。如下图所示，就是两个不同频率及振幅的波组合成一个新的波。

组合波

#The Importance of Composite Signals And Sine Functions

调制（Modulation）出来的信号通常是组合信号。数学家傅里叶(Fourier)发现可以从组合信号中解析出他的组成部分，即简单信号。大部分的通信系统都是用组合信号来携带信息，在接收端再将信息拆分成简单信号。

#Time And Frequency Domain Representations

之前的所有信号波的图片的 $X轴$ 都是时间，称为信号在时域(Time Domain)内表示。

还有一种表现方式是信号在频域(Frequency Domain)内的表示，如之前 $\sin (2\pi t)$ 和 $0.5\times \sin(2\pi 2 t)$ 组成的复合信号，也用下图在频域中表示：

频域表示

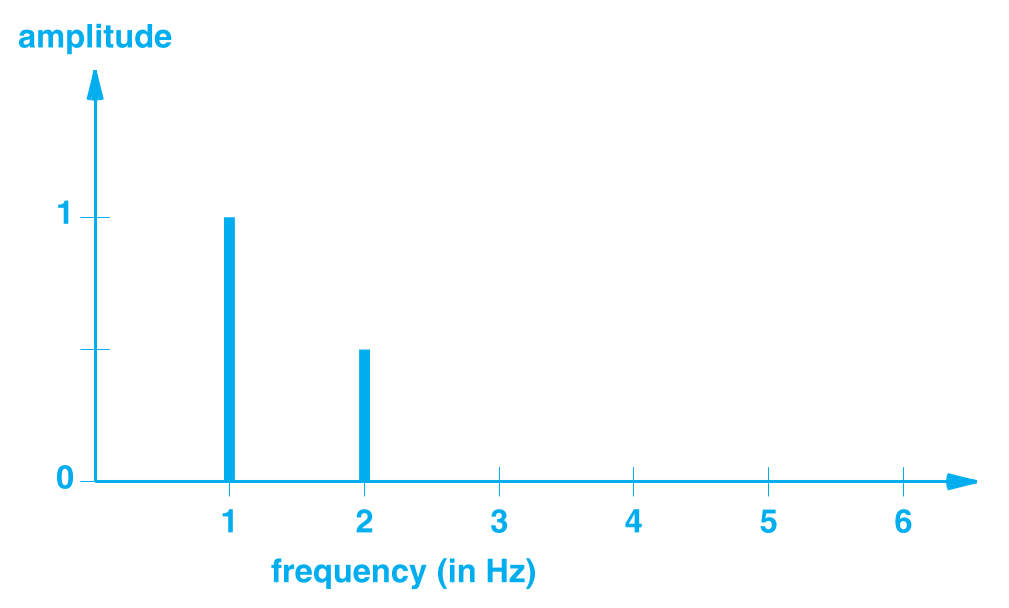
图中的 $x轴$ 为频率， $y$ 轴仍为波幅。可以看到在频率为 $1$ 和 $2$ 的地方有波形出现，正好对应函数 $\sin (2\pi t)$ 和 $0.5\times \sin(2\pi 2 t)$ 的频率，波形的振幅也与函数所表现的振幅相同。

因为每个简单波在频域图的 $x$ 轴上只占据一点，所以频域图用来表示复合波形是简单易读的。

#Bandwidth Of An Analog Signal

在计算机网络中经常听到网络带宽(Network Bandwidth)一词，关于网络带宽会在之后的章节中解释，这里先介绍一个相关概念，模拟带宽(Analog Bandwidth)。一个模拟信号的带宽是这个信号最高频率与最低频率之间的差，单位为 $Hz$ 。如一个信号的频域图如下图所示，那么这个信号的贷款为 $4KHz$ ，因为这个信号的最高频率为 $5KHz$ ，最低频率为 $1KHz$ 。

模拟带宽

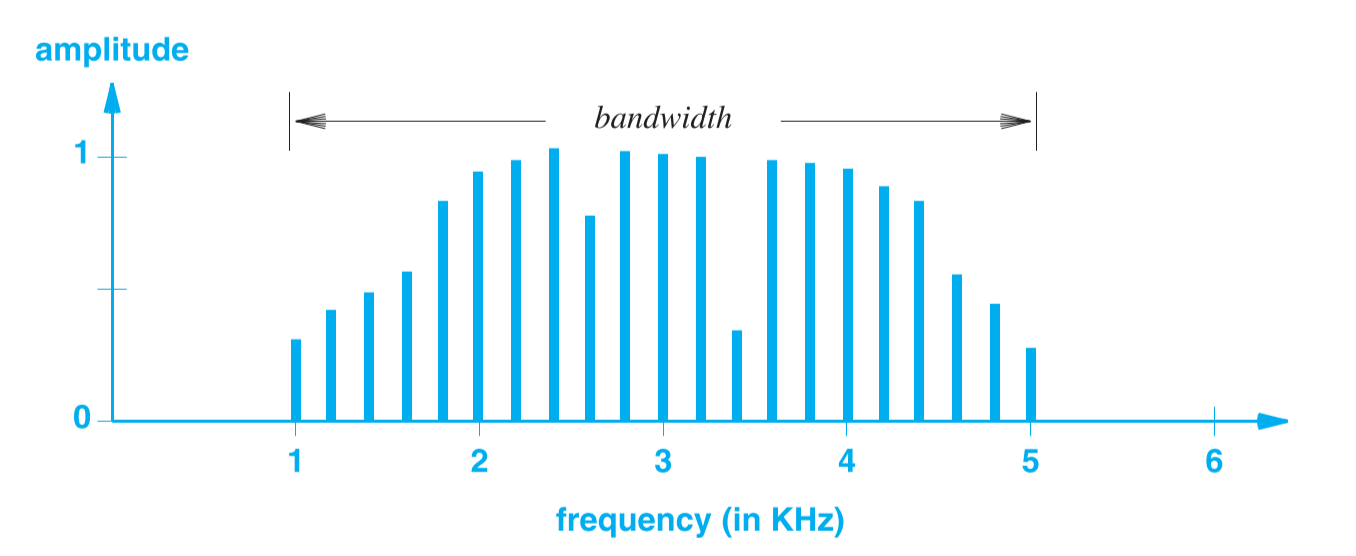
如果一个信号是用频域图来表示的，那么可以很快的看出这个信号的带宽。

#Digital Signals And Signal Levels

数字信号是由一系列的固定的 有效电平（Valid Level） 组成且在任意的时间点信号都处于这些有效电平之一。

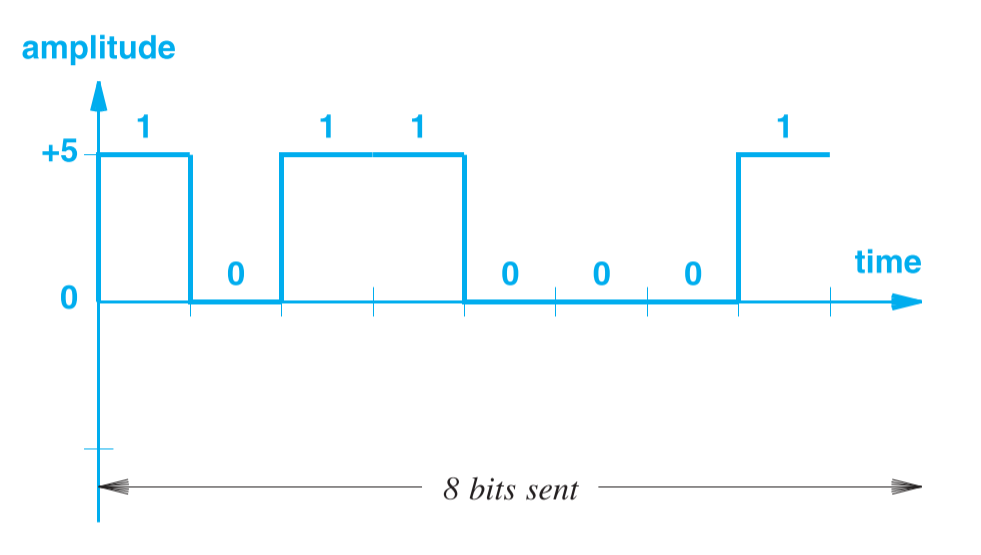
一些系统用电压来表示数字信号，如电压为 $5V$ 表示信号 1，电压为 $0V$ 表示信号 0，如下图所示：

电压信号1

如果将电压划分更细，如电压 $5V$ 表示信号 $11$ ，电压 $2V$ 表示 $10$ ，电压 $-2V$ 表示 $01$ ，电压 $-5V$ 表示 $00$ ，如下图所示：

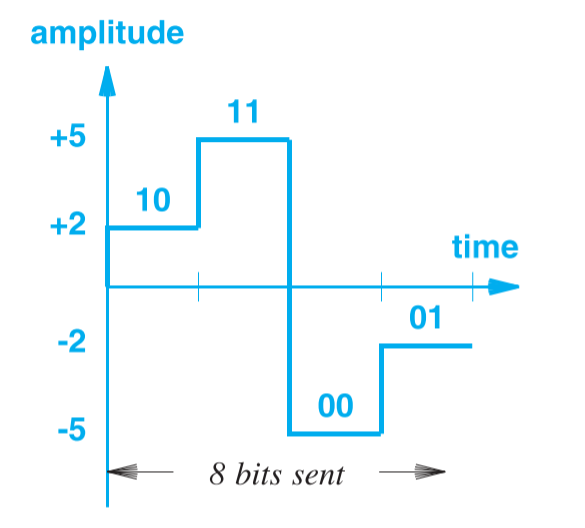
电压信号2

可以看到传输相同数据(8 bit)的情况下，第二种方法花费的时间少了一半，称第二种方法的 数据速率（Data Rate） 翻倍。因为第一种方法一次只能表示 1bit 的数据（1 或 0），而第二种方法表示了 2bit 的数据。如果电压细分为 $2^n$ 种，则一次性能表达 $n$ bit 的数据。

理论上可以将电压切分到非常小（如分割成一百万个电平等级）达到每次都能传递许多信息的目的，但是实际中因为电力系统并不能区分过小的电压间隔，所以只将电压分割为几个电平等级。

#Baud And Bits Per Second

数据速率有两方面决定，一方面是上一节中提到的信号有效电平数量（决定每次可以携带多少数据），另一方面是每个有效电平持续的时间。

如上一节中的例子，假设将 1 秒切分为 8 部分（即一秒电平可以变换 8 次）传递数据，一共有 2 个电平等级。那么一秒传递 8 bit 的数据。如果改为有 4 个电平等级，则每次能传递 2 个 bit,一秒传递 16 bit 的数据。如果仍然保持两个电平等级，但将一秒切分为 16 个部分，则同样一秒传递 16 bit 的数据。

将一秒电平可以变换的次数用波特表示(Baud)，波特数越高则一个电平持续的时间越短，如给每个电平 0.001 的持续时间，那么这个系统工作在 1000 Baud。理论上来说波特可以非常高，让每秒传递的数据增多，但是实际上当一个信号持续时间过短系统是无法检测到该信号的。每秒传递的数据量可用以下公式表示:

$\text{bits per second} = baud \times \lfloor \log_2{(levels)} \rfloor$

#Converting A Digital Signal To Analog

根据傅里叶定理，任意的波形都可以由一系列 Sin 波组成，其中每个 Sin 波都有各自的振幅，相位与频率。

数字信号也可以看作是一个跃变的波形，但是这样的跃变波形需要由无数个 Sin 波才能构成，所以从工程角度来说不可能实现，毕竟不可能找出无数个信源。

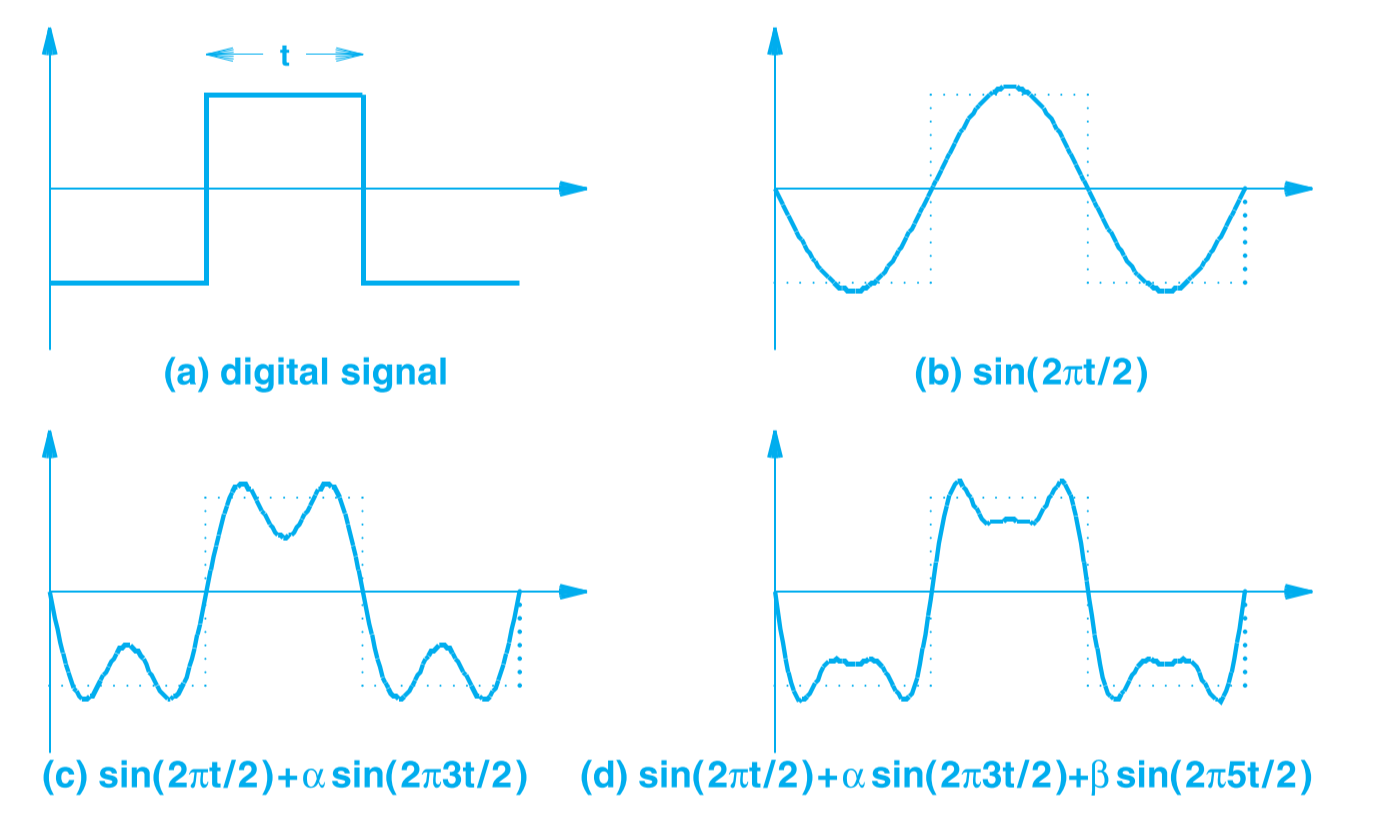
所以在实际运用中只能妥协，运用越多的 Sin 波形，最终的复合波形就越接近跃变波形。下图展示了用模拟信号来表示数字信号的过程，图（a）是数字信号，显示为跃变波形，图（b）是用一个 Sin 波来表示，图（C）是两个 Sin 波，图（d）是用三个 Sin 波。可以看到 Sin 波的数量越多，波形越接近跃变信号，而且新增的波的频率越来越高。

一般而言，用三个 Sin 波模拟即可。

数字电路转模拟电路

#The Bandwidth Of A Digital Signal

如之前所述，求一个信号的带宽是求其最大频率和最小频率的差值。对于数字信号来说可以先将他转换为模拟信号（多个 Sin 信号），然后找出最高频率的 Sin 以及最低频率的 Sin。但是如上节所述，数字信号的跃变波形是由无数的 Sin 组成，且 Sin 的频率越来越高，即数字信号的最高频率是无限，因此数字信号的带宽为无限。

#Synchronization And Agreement About Signals

在实际运用中，发送端和接收端必须保证信号的每次变换间隔是一样的（可看作采样频率），这个问题称为同步问题（Synchronization），下图展示了发送端和接收端以不同的频率采样会引发的问题，接收端的采样频率（10 次每秒）高于发送端（8 次每秒）。

采样错误

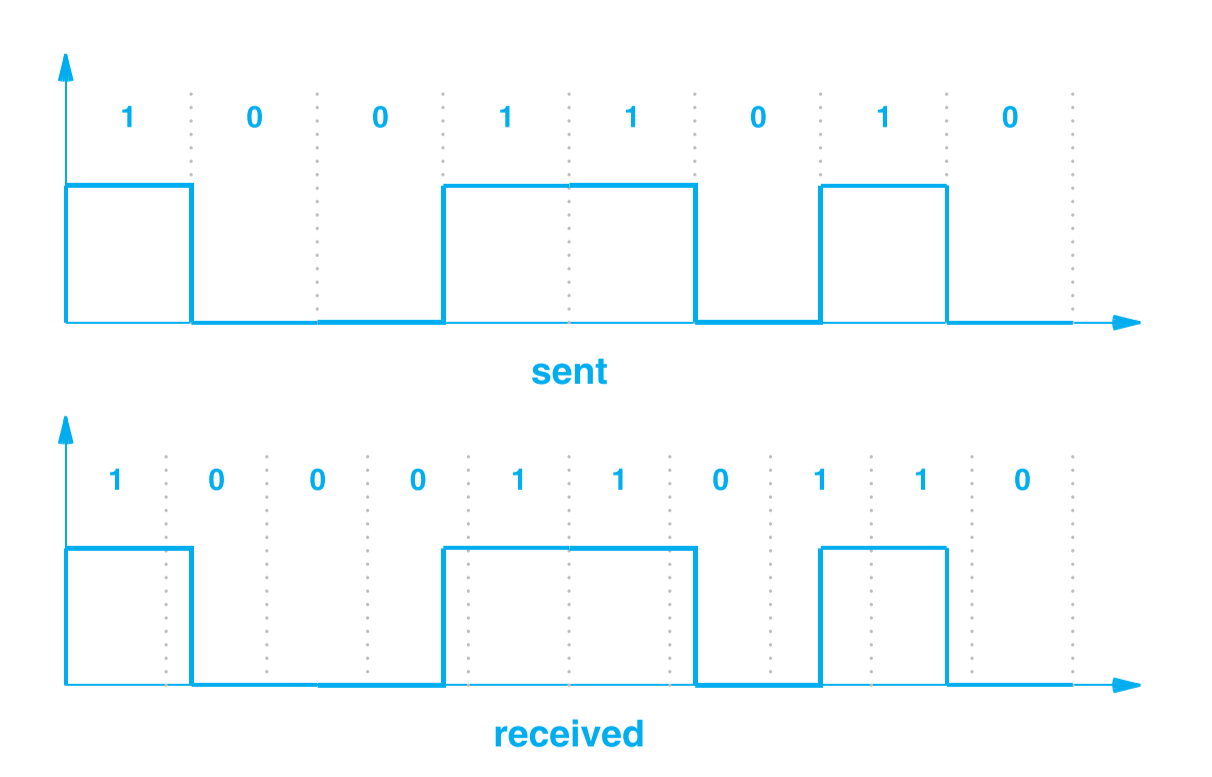
在实际运用中，这种频率的差异可能非常小，如误差为 $10_{-8}$ 秒，那可能出现了几百万个 Bit 后才发生一次错误。但在传输速率在亿个 Bit 每秒时，这种细微的差距也会引发大量的错误数据。

#Line Coding

如上节所述，在数据传递的过程中可能会因为同步问题导致一些错误的发生，有一些方法来帮助避免这些错误的发生。一种是真正发送信号前，先发送一系列的特定模式的字节，如重复的 0 或者重复的 1，通过这些字节来帮助接收端校准，另一种方法称为信道编码（Line Coding），在这种方式下会添加一些额外的字符来保证接收端能确切的解析出真实的数据。

如一个电路能产生 5V，0，-5V 的电压，可以将 -5V 定义为一个数据的开始。因此 0 信号表示为 $-5V, 0V$ ，1 信号表示为 $-5V, 5V$ 。接收端知道在-5V 信号后才是真正的数据。这种方式的图解如下：

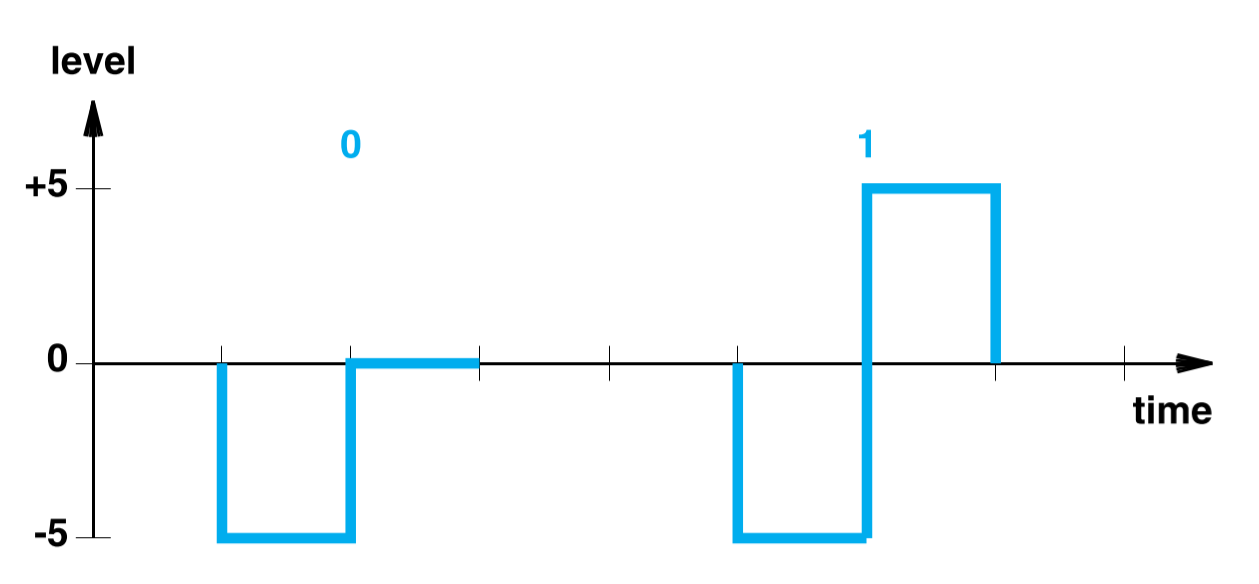
信道编码例子

因为信道编码引入了额外的数据来保证真实数据的准确性，所以信道编码降低了真实数据的传输速率。

#Manchester Encoding Used In Computer Networks

曼彻斯特编码(Manchester Encoding)是一种信道编码，在计算机网络中曼彻斯特编码主要用于以太网中，所以十分重要。

对电路来说，检测信号的变化比检测信号的强度要简单。因此曼彻斯特编码将 1 信号定义为从零电压跳转为正电压，将 0 信号定义为从正电压跳转为零电压。而且曼彻斯特采样的时间为时间周期的中间，因此可以对于连续 0 或者连续 1 的情况，信号有时间可以回到之前的电压水平，保证下一次的检测正常。曼彻斯特编码的图示如下：

曼彻斯特编码

曼彻斯特编码还有一个变化，叫做差分曼彻斯特编码（Differential Manchester Encoding），这种方法用相对变化来表示信号，0 信号表示信号发生了变化，1 信号表示信号没有变化。采样时间为时间周期点。差分曼彻斯特编码如下图所示：

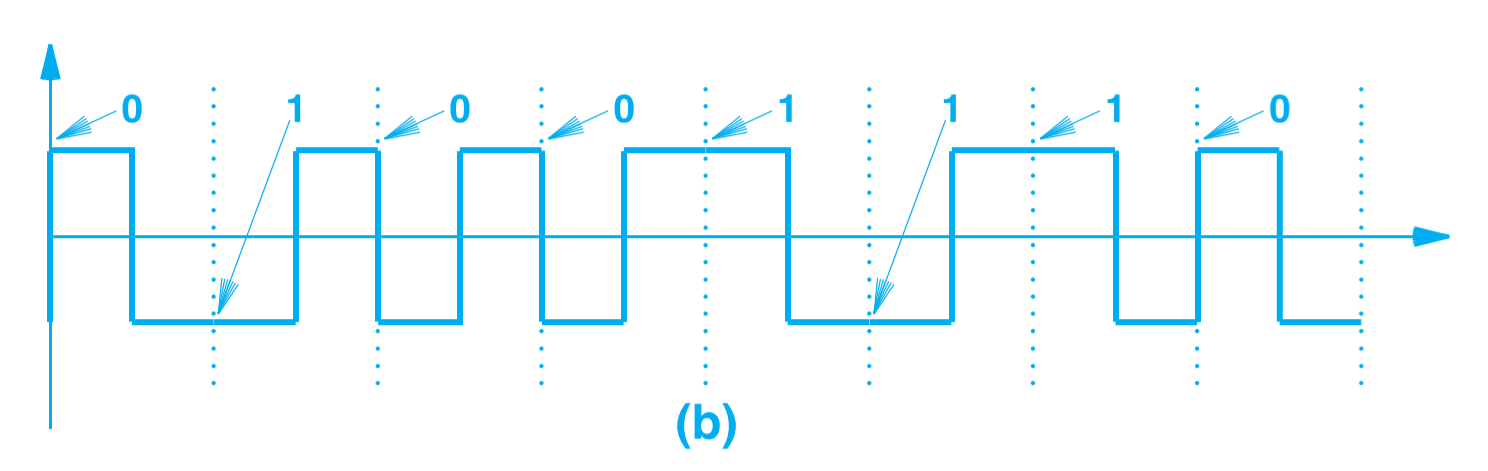
差分曼彻斯特编码

差分曼彻斯特编码的好处在于，即使信号的大小意外的翻转了也不会发生错误（如 5V 变为-5V 之类）。

#Converting An Analog Signal To Digital

模拟信号为了进一步的被处理，必须转换为数字信号。一般转换为数字信号有两种方式,一是 脉冲编码调制(Pulse Code Modulation，PCM)，另一种是 差分调制(Delta modulation)

脉冲编码调制是以相同时间间隔去测量模拟信号，并根据模拟信号的强度，将其转换为数字信号，整个流程分为三步，如下图框出的部分所示：

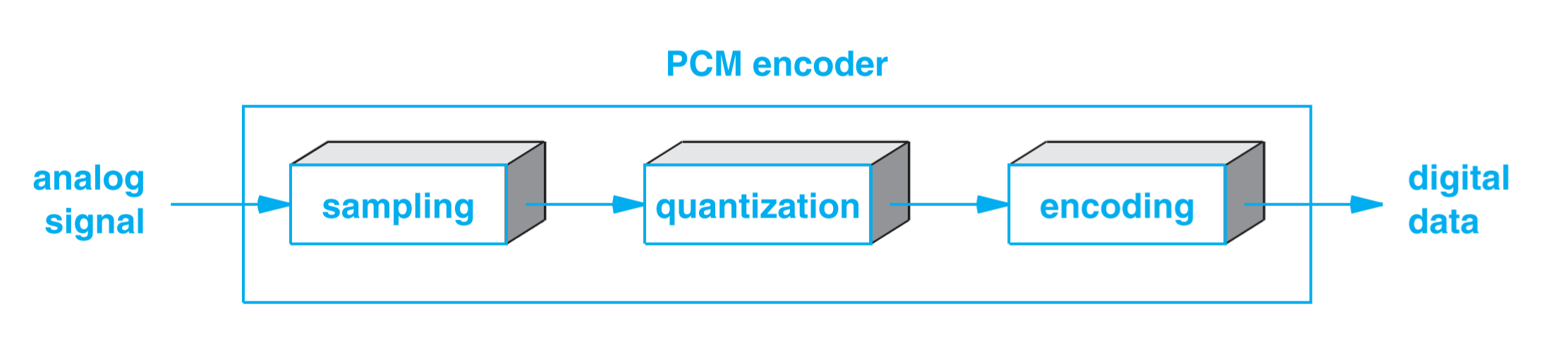
脉冲编码调制

以相同时间间隔去测量模拟信号，即为采样，所以上图中的第一部分称为采样。有的时候为了避免采样时间点的信号突变导致的采样失真，会在相关时间点附近多采样几次，然后取平均值作为最后采样值。第二部分称为量化（Quantization），量化是根据模拟信号的强度，将其转换为一个 Int 值，如下图所示，第一个采样的数值，会被量化为 2，第二个采样的数值会被量化为 3，第三个采样的数值会被量化为 6。

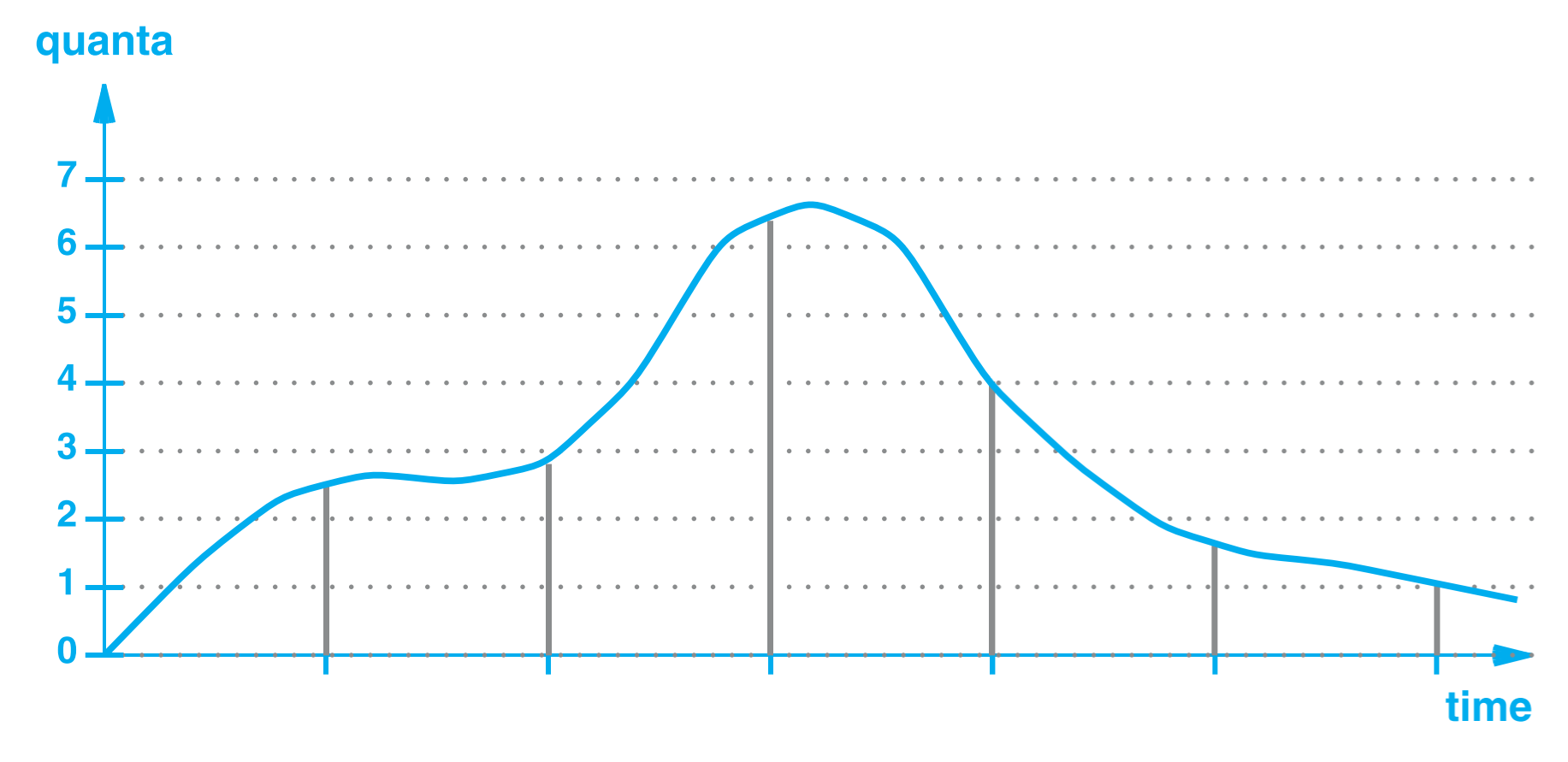
量化后的数据会被进一步编码为之后需要的数据格式（根据需求而定）。

差分调制的主题思想与脉冲编码调制类似，不同的是在量化阶段他不是对每个采样值进行量化，而是对当前采样值与上一个采样值的差距进行量化。这样节省了许多用来表示数据的 Bit 数，但是缺点在于一旦之前的数据出现了误差，后面的所有数据都会收到影响。

#The Nyquist Theorem And Sampling Rate

应该以怎样的采样频率进行采样是数据通信中需要考虑的问题，如果采样频率过低，那么采样出来的信号与原信号可能有较大差异，如果采样频率过高，则会产生大量的数据。

奈奎斯特（Nyquist Theorem）定理提出：为了避免采样失真，采样的最低频率应该是原信号最高频率的两倍。

#Nyquist Theorem And Telephone System Transmission

经过实验，0 到 4000HZ 的频率基本就能提供人所能接受的音频质量。因此根据奈奎斯特频率，语音信号的采样频率应该是 8000HZ，既一秒有 8000 个采样点。通话系统所用的 PCM 标准规定，每个采样信号用 8-bit 数据表示，所以每秒通话产生的数据量为：

$8000 \frac{samples}{second} \times 8 \frac{bits}{sample} = 64000 \frac{bits}{second}$

因此电话系统每秒传递 64000-bits 数据（64Kbps），也可见采样频率越高，可携带的数据也就越多。

#Nonlinear Encoding

当每个采样点只能用 8 个比特来表示时，线性的 PCM 编码无法很好的体现声音，因为 8 个 Bit 只能表现 256 个值，且线性表示的话，无论是非常低频或高频的部分还是人身大部分集中的部分都用了一样的采样间隔，这造成了浪费。而非线性编码，解决了这个问题，他更关注与人耳最敏感的频率。数字电话标准中有两种非线性编码：

$\alpha-law$ ，主要是欧洲及中国采用的编码方式
$\mu-law$ ，主要是北美和日韩采用的编码方式

$\mu-law$ 算法的主要优势在于它覆盖了更广的频率范围（例如可以更好的还原特别高的声音），缺点在于对于一些弱信号有更多的失真。 $\alpha-law$ 在弱信号的失真上有优势，但动态范围更小。

对于国际电话，需要有 $\alpha-law$ 和 $\mu-law$ 之间的转化。

#Encoding And Data Compression

数据压缩(Data Compression) 是用来减少用来表达数据的 bit 数的方法。对于数据通信来说，通常在传输前对数据进行压缩。压缩分为两种类型：有损压缩(Lossy)和无损压缩(Lossless)。

有损压缩则通常用来压缩一些人相关的文件，如图片，视频，音频，这种压缩方式会忽视掉一些人无法精确识别的数据，JPEG 和 MPEG-3(MP3) 都是典型的有损压缩。

无损压缩保证压缩后的数据在解压后与原数据相同，一般用于压缩文档之类的文件。大部分的无损压缩都用了字典技术，即如果一个字符串在文件中重复的出现，将这个字符串存放在字典中，之后的出现只要取字典中的索引值即可。