Normal Matrix 是用来将法线从 Model Space 转换到 World Spaces 的。

相对于将顶点位置从 Model Space 转换到 View Space，法线的转换有两点需要额外考虑：

  1. 法线是不需要考虑平移的
  2. 如果物体存在非等比例的缩放，而对法线直接进行这样的非等比例的缩放后，发现将不再垂直于平面，如下图所示：
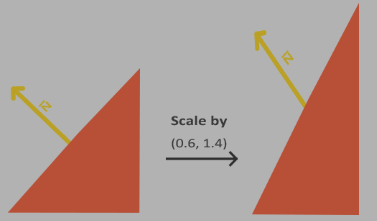
    错误的法线变化效果

因此 Normal Matrix 相较于普通的 Mode Matrix，需要对上述的情况做处理。

#排除平移

法线是一个方向，不需要考虑平移，因此 Model Matrix 中的平移部分是不需要的，只需要取 Model Matrix 的左上 3×33\times3 子矩阵即可。

即针对于法线，假设仍然使用 Model Matrix 来变换，那么表达式应该为：

1
normalOutput = normalize(mat3(model) * normalInput);

但这仅仅解决了平移的问题，对于非等比例缩放的问题，还需要进一步处理。

#处理非等比例缩放

#为何普通边可以使用 Model 矩阵

为了说明为何法线在使用 Model 矩阵转换后，遇到非等比例缩放下会出现问题，首先我们需要论证为何普通的边使用 Model 矩阵转换，在经过了非等比例缩放后，不会出现问题。

我们假设三角形的一条边上有 P1P_1 和 P2P_2 两个点，那么这条边可以表达为：

T=P2−P1T= P_2 - P_1

此时对这条边进行 Model Matrix 的变换，可以得到：

T′=M⋅T=M⋅(P2−P1)=M⋅P2−M⋅P1=P2′−P1′\begin{aligned} T^{\prime} & =M \cdot T \\ & =M \cdot\left(P_2-P_1\right) \\ & =M \cdot P_2-M \cdot P_1 \\ & =P_2^{\prime}-P_1^{\prime} \end{aligned}

由于 P1′P_1' 和 P2′P_2' 是三角形在转换后的两个顶点，因此 P2′−P1′P_2'-P_1' 仍然是转换后的三角形的边。

#为何法线不能使用 Model 矩阵

对于法线，我们可以同样用上述的方式计算，我们用 Q1Q_1 和 Q2Q_2 两个点来表示三角形的法线，假设 Q1Q_1 是三角形上的一个点， Q2Q_2 是三角形外的一个点，但两者的连线垂直于三角形的边：

N=Q2−Q1N = Q_2 - Q_1

在经过了 Model Matrix 的变换后，我们得到：

N′=Q2′−Q1′N' = Q_2' - Q_1'

此时，我们只能保证 Q1′Q_1' 是三角形上的一个点，但 Q2′Q_2' 和 Q1′Q_1' 之间的连线，即 N′N' 并不能确定是垂直于三角形的边的。

如果要确保 N′N' 仍然垂直于三角形的边，那么必须满足 N′⋅T′=0N' \cdot T' = 0。我们前面已经知道了 T′T' 是通过 TT 经由 MM 矩阵变换得到，而满足条件的 N′N' 不一定可以通过矩阵 MM 变换获得。我们这里假设满足条件的 N′N' 可以通过矩阵 GG 变换得到，即：

N′⋅T′=(GN)⋅(MT)=0\begin{aligned} N' \cdot T' &= (GN) \cdot (MT) \\ &= 0 \end{aligned}

我们要求的就是矩阵 GG 该如何表达。

上述公式的 GNGN 和 MTMT 都是向量，表达式求的是两个向量的点积。为了方便后续的计算，我们首先需要将 GNGN 和 MTMT 间的计算转换为矩阵的乘法。假设 NN 和 TT 都是行向量，那么 GNGN 和 MTMT 也是行向量，为了让 GNGN 和 MTMT 可以用矩阵乘法表示，需要首先将 GNGN 转换为列向量，这需要对 GNGN 进行转置，即：

(GN)⋅(MT)=(GN)T(MT)(G N) \cdot(M T)=(G N)^T(M T)

同理对于向量计算 N⋅T=0N \cdot T = 0 也可以转换为矩阵运算 NTT=0N^TT=0

上述式子可以进一步化简为：

(GN)T(MT)=NTGTMT(G N)^T(M T)=N^T G^T M T

将上述的计算连起来，即我们需要求 GG，GG 满足：

N′⋅T′=NTGTMT=0N' \cdot T' = N^T G^T M T= 0

假设 GTM=IG^TM = I，那 NTGTMTN^T G^T M T 就变为了 NTTN^TT，NTTN^TT 显然是等于 0 的，即满足了我们的要求。

NTN^T 即为变化前的三角形的法线的矩阵表示，T 即为变换前的三角形的边，他们相乘显然为 0。

此时问题就变成了求 GG，而 GG 满足 GTM=IG^TM = I：

GTM=IGT=M−1G=(M−1)T\begin{aligned} G^TM &= I \\ G^T &= M^{-1} \\ G &= (M^{-1})^T \end{aligned}

至此我们求得了 GG，即对于法线，我们需要使用 (M−1)T(M^{-1})^T 来变换。

所以一个正确的法线变换的表达式为：

1
normalOutput = normalize(mat3(transpose(inverse(model))) * normalInput);

#Reference

The Normal Matrix » Lighthouse3d.com