针对对于任意轴的旋转矩阵，思路同样是求基本向量在旋转后的结果。

向量v\mathbf{v}在绕任意轴 nn 旋转θ\theta角度后变为 v′\mathbf{v^{'}}，表达式为：

v′=vR(n^,θ)\mathbf{v^{'}}=\mathbf{v}\mathbf{R}(\hat{\mathbf{n}},\theta)

为了方便计算，将向量 v\mathbf{v} 拆成两部分 v∥\mathbf{v}_{\parallel} 和 v⊥\mathbf{v}_{\perp}，分别表示平行于和垂直于旋转轴 n\mathbf{n} 的分量。在旋转过程中，平行于旋转轴 n\mathbf{n} 的分量 v∥\mathbf{v}_{\parallel} 是不会发生变化的，因此要求的只是旋转后的 v⊥′\mathbf{v}^{'}_{\perp} 。示意图如下：
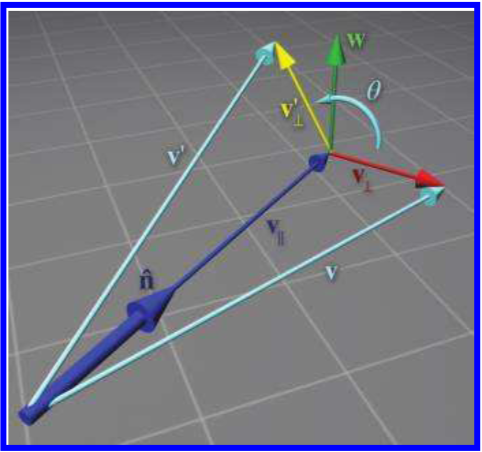
拆分向量 V

  • v∥\mathbf{v}_{\parallel}可以通过点积求得，即v∥=(v⋅n^)n^\mathbf{ v_{\parallel}=(\mathbf{v}\cdot \hat{\mathbf{n}})\hat{\mathbf{n}}}
  • v⊥\mathbf{v}_{\perp}可以通过v\mathbf{v}减去v∥\mathbf{v}_{\parallel}得到，即 v⊥=v−v∥\mathbf{v_{\perp}=\mathbf{v}-\mathbf{v}_{\parallel}}
  • w\mathbf{w} 向量是为了与向量 v⊥\mathbf{v}_{\perp} 构成一个平面，w\mathbf{w} 向量的长度与v⊥\mathbf{v}_{\perp} 相同，且垂直于n^\hat{\mathbf{n}}和v⊥\mathbf{v}_{\perp}，所以可得w=n^×v⊥\mathbf{w}=\hat{\mathbf{n}}\times \mathbf{v}_{\perp}
  • 此时，w\mathbf{w} 和 v⊥\mathbf{v}_{\perp} 构成了一个二维平面，根据二维平面的旋转可得，v⊥′=cos⁡θv⊥+sin⁡θw\mathbf{v}_{\perp}^{'}=\cos \theta \mathbf{v}_{\perp} + \sin\theta \mathbf{w}

如果两个坐标轴是单位向量，则旋转 θ\theta 角度的结果为 (cos⁡θ,sin⁡θ)(\cos \theta, \sin \theta)。而这里两个坐标轴分别是 v⊥\mathbf{v}_{\perp} 和 w\mathbf{w} ，因此结果为：cos⁡θv⊥+sin⁡θw\cos \theta \mathbf{v}_{\perp} + \sin\theta \mathbf{w}

  • 结合上面所有的式子，可推导出v′\mathbf{v}^{'}的公式，即

v′=v⊥′+v∥=cos⁡θv⊥+sin⁡θw+(v⋅n^)n^=cos⁡θ(v−(v⋅n^)n^)+sin⁡θ(n^×v⊥)+(v⋅n^)n^=cos⁡θ(v−(v⋅n^)n^)+sin⁡θ(n^×(v−v∥))+(v⋅n^)n^=cos⁡θ(v−(v⋅n^)n^)+sin⁡θ(n^×v−n^×v∥)+(v⋅n^)n^=cos⁡θ(v−(v⋅n^)n^)+sin⁡θ(n^×v−0)+(v⋅n^)n^=cos⁡θ(v−(v⋅n^)n^)+sin⁡θ(n^×v)+(v⋅n^)n^\begin{aligned}\mathbf{v}^{'} &= \mathbf{v}_{\perp}^{'}+\mathbf{v}_{\parallel}\\&=\mathbf{\cos \theta v_{\perp} + \sin\theta w+(v\cdot\hat{n})\hat{n}} \\&=\cos\theta(\mathbf{v}-(\mathbf{v}\cdot\hat{\mathbf{n}})\hat{\mathbf{n}})+\sin\theta (\hat{\mathbf{n}}\times \mathbf{v}_{\perp})+(\mathbf{v}\cdot\hat{\mathbf{n}})\hat{\mathbf{n}} \\&=\cos\theta(\mathbf{v}-(\mathbf{v}\cdot\hat{\mathbf{n}})\hat{\mathbf{n}})+\sin\theta (\hat{\mathbf{n}}\times(\mathbf{v}-\mathbf{v}_{\parallel}))+(\mathbf{v}\cdot\hat{\mathbf{n}})\hat{\mathbf{n}} \\&=\cos\theta(\mathbf{v}-(\mathbf{v}\cdot\hat{\mathbf{n}})\hat{\mathbf{n}})+\sin\theta (\hat{\mathbf{n}}\times \mathbf{v}-\hat{\mathbf{n}} \times \mathbf{v}_{\parallel})+(\mathbf{v}\cdot\hat{\mathbf{n}})\hat{\mathbf{n}} \\&=\cos\theta(\mathbf{v}-(\mathbf{v}\cdot\hat{\mathbf{n}})\hat{\mathbf{n}})+\sin\theta (\hat{\mathbf{n}}\times \mathbf{v}-0)+(\mathbf{v}\cdot\hat{\mathbf{n}})\hat{\mathbf{n}} \\&=\cos\theta(\mathbf{v}-(\mathbf{v}\cdot\hat{\mathbf{n}})\hat{\mathbf{n}})+\sin\theta (\hat{\mathbf{n}}\times \mathbf{v})+(\mathbf{v}\cdot\hat{\mathbf{n}})\hat{\mathbf{n}} \end{aligned}

即最终用n^，θ，v\hat{\mathbf{n}}，\theta，\mathbf{v}表达v′\mathbf{v}^{'}的式子为：

v′=cos⁡θ(v−(v⋅n^)n^)+sin⁡θ(n^×v)+(v⋅n^)n^v^{'}=\cos\theta(\mathbf{v}-(\mathbf{v}\cdot\hat{\mathbf{n}})\hat{\mathbf{n}})+\sin\theta (\hat{\mathbf{n}}\times \mathbf{v})+(\mathbf{v}\cdot\hat{\mathbf{n}})\hat{\mathbf{n}}

首先将 v\mathbf{v} 以数值 [100]\begin{bmatrix} 1 & 0& 0\end{bmatrix} 代入，可得：

v′=cos⁡θ([100]T−nx[nxnynz]T)+sinθ[0n_z−n_y]T+nx[nxnynz]T\mathbf{v}^{'}=\cos\theta({\begin{bmatrix} 1\\\\0\\\\0 \end{bmatrix}}^T-\mathbf{n}^x{\begin{bmatrix} \mathbf{n}^x\\\\\mathbf{n}^y\\\\\mathbf{n}^z \end{bmatrix}}^T)+sin\theta {\begin{bmatrix} 0\\\\\mathbf{n}\_z\\\\-\mathbf{n}\_y \end{bmatrix}}^T+\mathbf{n}^x{\begin{bmatrix} \mathbf{n}^x\\\\\mathbf{n}^y\\\\\mathbf{n}^z \end{bmatrix}}^T

其中：n^=[nxnynz]T\hat{\mathbf{n}}={\begin{bmatrix} n^x\\\\n^y\\\\n^z \end{bmatrix}}^T，且 n^×v=[0nz−ny]T\hat{\mathbf{n}}\times \mathbf{v}={\begin{bmatrix} 0\\\\n^z\\\\-n^y \end{bmatrix}}^T

原式可继续简化得：

v′=cos⁡θ([100]T−nx[nxnynz]T)+sinθ[0nz−ny]T+nx[nxnynz]T=[cos⁡θ(1−nx2)+0+nx2cos⁡θ(0−nxny)+sin⁡θnz+nxnycos⁡θ(0−nxnz)−sin⁡θny+nxnz]T=[nx2(1−cos⁡θ)+cos⁡θnxny(1−cos⁡θ)+nzsin⁡θnxnz(1−cos⁡θ)−nysin⁡θ]T\begin{aligned}\mathbf{v}^{'} &=\cos\theta({\begin{bmatrix} 1\\\\0\\\\0 \end{bmatrix}}^T-n^x{\begin{bmatrix} n^x\\\\n^y\\\\n^z \end{bmatrix}}^T)+sin\theta {\begin{bmatrix} 0\\\\n_z\\\\-n_y \end{bmatrix}}^T+n^x{\begin{bmatrix} n^x\\\\n^y\\\\n^z \end{bmatrix}}^T \\&={\begin{bmatrix}\cos\theta(1-{n_x}^2)+0+{n_x}^2\\\\\cos\theta(0-n_xn_y)+\sin\theta n_z+n_xn_y\\\\\cos\theta(0-n_xn_z)-\sin\theta n_y +n_xn_z\end{bmatrix}}^T \\&={\begin{bmatrix}{n_x}^2(1-\cos \theta) + \cos\theta \\\\n_xn_y(1-\cos \theta)+n_z\sin\theta \\\\n_xn_z(1-\cos \theta) -n_y\sin\theta\end{bmatrix}}^T \end{aligned}

该结果即为最终求得矩阵的一行，使用相同的步骤可以求得剩下两行，即

当 v\mathbf{v} 以数值 [010]\begin{bmatrix} 0 & 1& 0\end{bmatrix} 代入，可得

v′=[nxny(1−cos⁡θ)−nzsin⁡θny2(1−cos⁡θ)+cos⁡θnynz(1−cos⁡θ)+nxsin⁡θ]T\mathbf{v}^{'}={\begin{bmatrix}n_xn_y(1-\cos \theta) -n_z\sin\theta \\\\{n_y}^2(1-\cos \theta)+\cos\theta \\\\n_yn_z(1-\cos \theta) +n_x\sin\theta\end{bmatrix}}^T

当 v\mathbf{v} 以数值 [001]\begin{bmatrix} 0 & 0& 1\end{bmatrix} 代入，可得

v′=[nxnz(1−cos⁡θ)+nysin⁡θnynz(1−cos⁡θ)−nxsin⁡θnz2(1−cos⁡θ)+cos⁡θ]T\mathbf{v}^{'}={\begin{bmatrix}n_xn_z(1-\cos \theta) +n_y\sin\theta \\\\n_yn_z(1-\cos \theta)-n_x\sin\theta \\\\{n_z}^2(1-\cos \theta) +\cos \theta\end{bmatrix}}^T

至此，得到了绕任意轴 nn 旋转 θ\theta 角度矩阵的三行数据，合并在一起可得：

R(n^,θ)=[nx2(1−cos⁡θ)+cos⁡θnxny(1−cos⁡θ)+nzsin⁡θnxnz(1−cos⁡θ)−nysin⁡θnxny(1−cos⁡θ)−nzsin⁡θ ny2(1−cos⁡θ)+cos⁡θnynz(1−cos⁡θ)+nxsin⁡θnxnz(1−cos⁡θ)+nysin⁡θnynz(1−cos⁡θ)−nxsin⁡θnz2(1−cos⁡θ)+cos⁡θ]R({\hat{n},\theta})=\begin{bmatrix}{n_x}^2(1-\cos \theta) + \cos\theta &n_xn_y(1-\cos \theta)+n_z\sin\theta &n_xn_z(1-\cos \theta) -n_y\sin\theta\\\\n_xn_y(1-\cos \theta) -n_z\sin\theta  &{n_y}^2(1-\cos \theta)+\cos\theta &n_yn_z(1-\cos \theta) +n_x\sin\theta\\\\n_xn_z(1-\cos \theta) +n_y\sin\theta &n_yn_z(1-\cos \theta)-n_x\sin\theta &{n_z}^2(1-\cos \theta) +\cos \theta\end{bmatrix}