分辨率 是个我们非常熟悉的的词汇，我们会说一张图片的分辨率是 1920x1080，或者说一个显示器的分辨率是 4K。我们总是很本能的认为分辨率很重要，且常常认为分辨率越高越好，但事实确实如此吗。这篇文章会从技术细节的角度去阐述分辨率究竟是什么，以及为何分辨率对显示效果如此的重要，即我们目标回答三个问题：

分辨率是什么？
为何分辨率如此重要？
分辨率越高越好吗？

以照片为例，当我们拍摄了一张照片，并说这个照片的分辨率是 $1920\times 1080$ 时，我们实际上是在描述这张照片的像素数， $1920\times1080$ 表示这张照片的宽度有 1920 个像素，高度有 1080 个像素。

这里的每一个像素都是我们在拍照时，相机对真实世界的 采样 结果。所以，为了更好的理解分辨率，我们需要先了解 采样 的概念。

#什么是采样

采样是指在一个连续的信号中，选择离散的点来代表这个信号，这个解释无疑又引入了两个概念：信号 和 离散。

当想要尽可能准确而又彻底的解释一个概念时，通常会不幸的发现，需要解释的概念会越来越多。

#什么是离散信号

信号是指在时间或空间上变化的物理量，例如你听到的声音，你看到的颜色，或者你触摸到物体的感受，他们都是信号。在真实世界里，信号都是连续的。我们可以举一个非常极端的简化场景，你在一个完全黑色的房间内，看着一堵墙，墙的颜色从左至右分别是纯粹的黑，然后均匀逐渐变为纯粹的白，再逐渐变为纯粹的黑。

那么你视野中会看到一段连续的黑色，然后逐渐变换为白色，然后再逐渐变换为黑色，如果我们通过一个函数图来描述你的视野，那么会是这样一张图，其中 X 轴表示你视野从左至右，Y 轴表示颜色，0 是黑色，1 是白色：

视野中的黑白

无疑，你视野中看到的内容是连续的，所以这里的图形也是连续的，这里用数值表示的颜色即是一个连续的信号。

当你在这个房间内用手机拍了一张照片时，并在电脑上查看照片时，乍一眼看，你会觉得照片上的黑白变换同样是均匀且连续的，但你将照片放大后。你会发现你看到了一个个纯色的色块，颜色是以“色块”为最小单位变换的，这些色块就是照片的像素，所以照片并不是“均匀”连续变换的，而是以像素为单位跳跃着变换的，即它是离散的。

同样的，如果以函数图来表示照片中的颜色变化，那么就会变成这样，其中每一个小点即表示一个像素：

当你看照片的时候，你会觉得照片中的颜色变化是连续的，这是因为你的大脑做了一个类似于将离散信号还原为连续信号的过程，即你的大脑会将上述图中的一个个小点连接起来，形成一条连续的曲线。

#采样频率

在上一节中，我们通过两个例子说明了连续信号（你的视野）和离散信号（照片）之间的区别，采样就是让连续信号变为离散信号的过程。

采样最关键的信息，是采样的 间隔，间隔可能是均匀的，也可能是不均匀的。均匀采样是指在连续信号中，按照固定的间隔来选择点，而不均匀采样则是按照不规则的间隔来选择点。

当用图片来表示时，图片中的每一个像素的大小是相同的，所以图片是均匀采样的。

分辨率即是每一个方向上的采样次数，分辨率越高也就意味着每个方向上的采样点数越多。

当采样是均匀采样时，采样中最关键的信息就成为了采样的频率，即每单位长度内采样的点数。采样频率越高，间隔越短，同等长度下采样的点数就越多，离散信号也就越接近于连续信号。

所以问题 “为什么分辨率很重要”，可以等效为“为什么采样频率很重要”。

从一张照片的分辨率角度出发，如果你拍摄的焦距和视角是固定的，那么“单位长度”就是相机的采景框中你所能看到的内容，对于使用相同焦距的一系列照片，一张照片的分辨率越高，即意味着这张照片的采样频率越高。
请注意，这里强调了 “焦距”的概念，这是因为采样频率不仅仅取决于采样的次数，还取决于采样的范围。即一个照片的采样频率由两部分决定：

焦距：焦距决定了你拍摄的视角范围，焦距越长，视角范围越小。对于分辨率相同的情况下，焦距越长，采样频率就越高。
分辨率：分辨率决定了每个方向上的采样点数。对于焦距相同的情况下，分辨率越高，采样频率就越高。

对于虚拟渲染而言，与焦距类似的概念是 FOV，渲染的内容多少受 FOV 影响：

当分辨率相同时，FOV 越大，采样频率越低
当 FOV 相同时，分辨率越高，采样频率越高

在上一节的例子中，因为采样的频率不算低，所以我们根据离散信号，是能够很本能的还原出连续信号的，但如果采样的频率过低，那么则无法正确的还原连续信号。

同样的，我们可以举一个极端的例子，还是在这个纯黑并有一堵黑白渐变墙的房间，假设我们用一张分辨率为 $1\times 1$ 的照片来拍摄这个墙，那么我们得到的照片使用函数绘制会是这样的：

一像素

无疑，当你看着这张只有 1 像素的照片时，无论如何，你的大脑都无法将其还原为连续的黑白渐变曲线。所以这里，1 像素的图片是无法还原原始的连续信号的。但是，假设房间是纯粹的黑色，而墙也是纯粹的黑，即你的视野中看到的都是纯粹的黑色，那么这个 1 像素的照片，同样满足你的视野中看到的内容。

在这两个例子中（纯黑的房间内有一个颜色连续变化的墙 vs 纯黑的房间内有一个纯黑的墙），我们使用了相同的焦距的拍摄了两张都是分辨率为 $1\times 1$ 的照片，但在第一个例子中，我们无法还原出连续信号，而在第二个例子中，我们可以还原出连续信号。

无疑，这个例子说明了采样频率并不是唯一的因素，原始信号的内容同样会影响我们是否能还原出准确的连续信号。那么有一个问题就会冒出来“对于一个恒定的采样频率，它能还原哪些原始信号”，这个问题的答案是：采样定理。

#采样定理

采样定理是一个数学定理，它描述了如何从离散信号中恢复连续信号。采样定理的核心内容是：如果一个连续信号的最高频率为 $f_{max}$ ，如果以大于或等于 $2f_{max}$ 的频率进行采样，就可以完全恢复这个信号。这里的 $2f_{max}$ 也被称为 奈奎斯特频率（Nyquist frequency）。

从采样定理中可以看出，采样结果是否能正确还原连续信号，取决于两部分：

原始信号的最高频率是多少
采样频率是否足够高

我们已经知道对于一张焦距固定的图片而言，采样频率就是分辨率，此时剩下的问题是，我该如何知道真实世界中的信号的最高频率是多少呢？比如在我们的例子中，对于一个黑白渐变的墙面，即使我用一个函数图像画出了它渐变的样子（参考上面的绘制的连续信号函数图），我又该如何知道这个函数的最高频率呢？

问题的解答是 傅里叶变换（Fourier Transform）。

#傅里叶变换

傅里叶变换是一个数学工具，它可以将一个任意连续信号分解为一组正弦波的叠加。通过傅里叶变换，我们可以将任意一个信号拆分为多个不同频率的正弦波，这些正弦波中频率最高的那个即为这个信号的最高频率。

例如以下的一个连续信号：

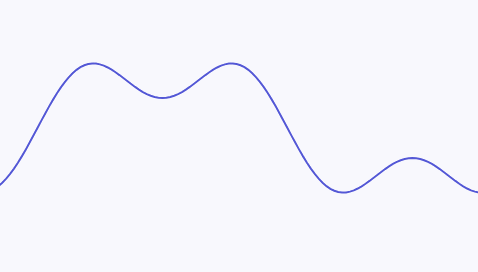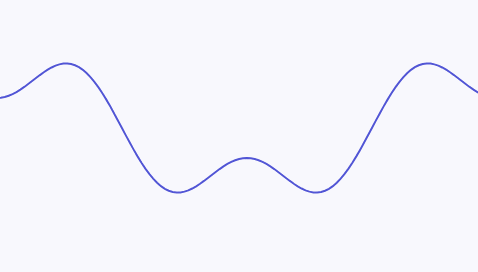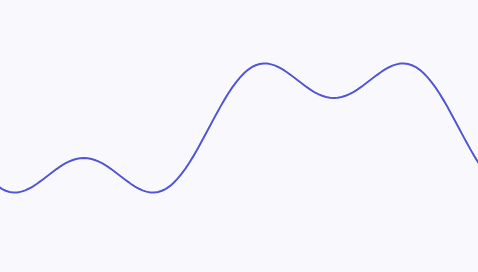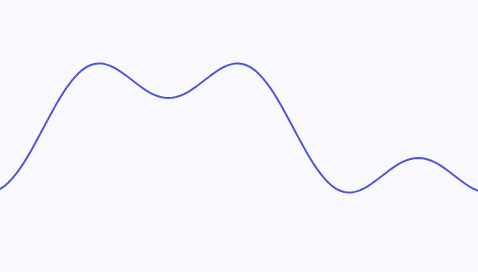
可以拆分为两个不同频率的正弦波的叠加。其中图例中下方的正弦波有着更高的频率，这个连续信号的最高频率即为下方的正弦波的频率：

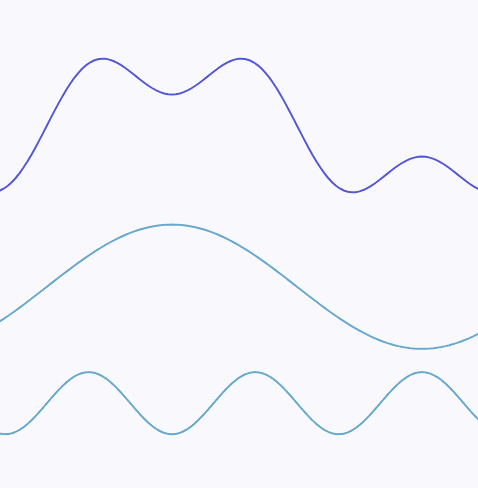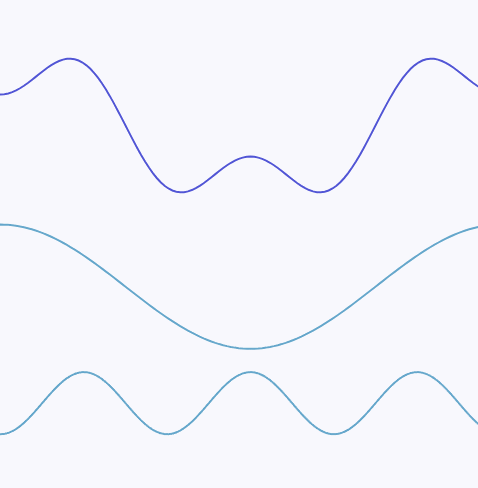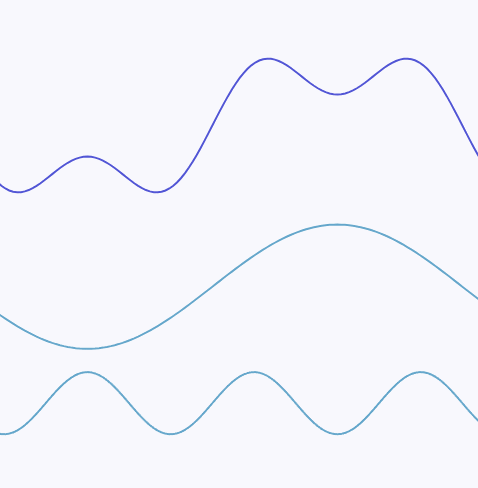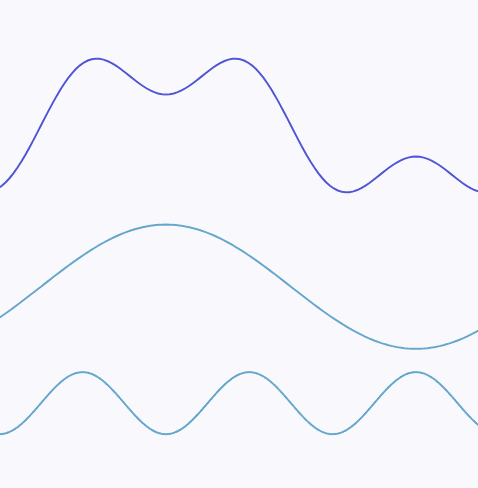
越是尖锐的变化，频率就越高，最尖锐的变换无疑就是一个垂直的线段，如下为一段包含有近似垂直线段的连续信号：

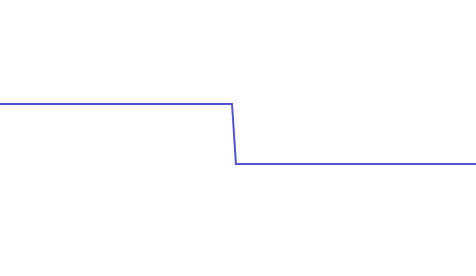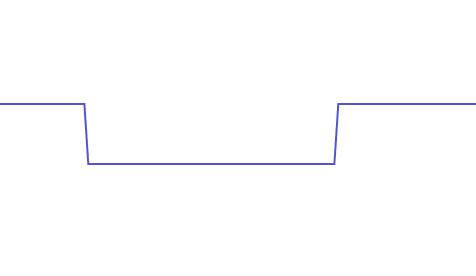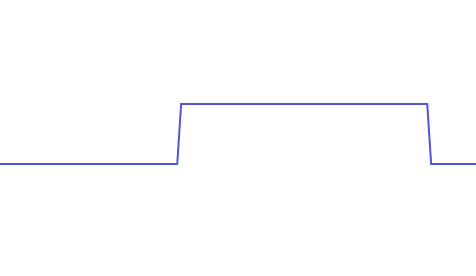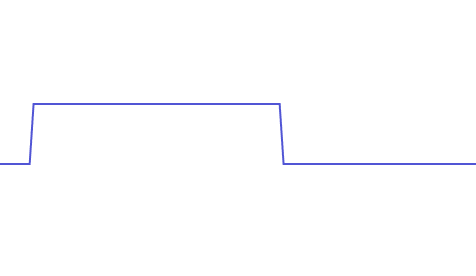
为了能正确的复原这段信号，我们需要有一系列的正弦波叠加，而随着叠加的正弦波频率越高，我们就越能复现这个连续信号，这个连续信号的最高频率即为其完美复现时所叠加的最高频率的正弦波：

从上述的示例中，不难看出，对于一个信号，它变换的越快，想要复原它就需要越高频率的正弦波，也即意味着它的最高频率越高，也意味着需要越高的采样频率来还原这个原始信号。

在我们的日常生活中，我们通过 “细节” 这个词来描述快速的变化的部分，对于细节多的内容，我们通常需要更高的采样频率（同焦距/FOV 下，即更高的分辨率）。

还是以房中之墙为例，如果房间与墙壁都是纯粹的黑，那么你的视野内是没有任何的变化的，无疑这时没有任何的细节。而当那堵墙存在变化时，它变化的越快，你需要察觉的“细节”就越多。

正因为人对于变化快的内容更难察觉，所以才会用“细节”这个词去描绘。

#总结

至此，我们已经拥有了从信号角度去解析分辨率的所有工具，文章一开始的三个问题，在之前的论述中都已经解答了，现在我们再次总结下回答：

分辨率是什么？

分辨率是一张图片上每个方向上的采样点数，分辨率越高即意味着每个方向上的采样点数越多。在图片所要展现的内容固定的情况下，分辨率越高意味着对所要展现的内容的采样频率越高，也因此意味着对于所要展现的内容的还原越准确。
为何分辨率如此重要？

因为分辨率越高通常意味着采样频率越高，而采样频率越高就意味着我们可以还原的信号的频率越高，也就意味着我们可以还原的细节越多。
分辨率越高越好吗？

如上所属，分辨率越高越能还原原始的内容，所以在不考虑成本的前提下，分辨率是越高越好的。

但如果考虑成本，则分辨率的高低需要取决于它所展现的内容的细节程度，即内容的频率。对于一个内容的频率越高的内容，分辨率就需要越高才能正确还原这个内容；而对于一个内容的频率较低的内容，分辨率就可以相对较低。

在分辨率固定的情况下，降低内容的频率（即降低内容的细节）也可以让我们准确的还原出内容。

我们也能解释一些虚拟渲染时，常见的现象：

图片中黑白突变的部分容易出现锯齿/摩尔纹
图像中黑色到白色的突变，即是一个垂直的变化（从 0 → 1），由上所述，可以知道这个变化所蕴含的频率极高。
也因此，这种黑白图标的图片在被渲染时容易出现锯齿/摩尔纹，因为渲染时的采样频率（由分辨率和 FOV 共同决定）已经无法满足原始信号（黑白突变）的最高频率。
锯齿总是出现在物体的边缘

因为物体的边缘通常是一个快速变化的部分（A 物体和 B 物体放在一起， A 物体的边缘意味着 A 物体的颜色与 B 物体的颜色之间的突变），即它的频率较高。由于渲染时的采样频率无法满足这个频率，所以会出现锯齿。

希望这篇文章能让你更了解分辨率，其中的几个结论你需要牢记于心，这对你理解与优化一些显示效果至关重要：

分辨率与采样频率强相关
原始信号的频率与采样频率是否匹配，直接决定了采样后的结果是否可以还原原始信号
- 采样频率受采样次数（分辨率）和采样范围（焦距）影响
- 原始信号频率受内容细节影响
越细节的内容就表示原始信号的频率越高，采样频率需要越高才能还原出原始信号

#Reference

An Interactive Introduction to Fourier Transforms：文章中的傅里叶变换说明主要来自于此，在这个网站中，你也可以绘制任意的曲线来进行傅里叶展开。